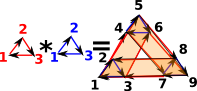On the page about graph theory here we see that there are two ways we can take the product of graphs, the tensor product and the Cartesian product. Since simplicial complexes are a generalisation of graphs I would like to find and equivalent of these products for simplicial complexes.
see Hatcher
- page 277 - The simplical cross product.
- page 278 - The cohomology cross product.
Products of Facets
Before we can calculate the products of whole simplicial complexes we need to be able to calculate the products of individual facets.
Simplexes as an Extension of Graphs
When we looked at the product of graphs, on this page, we saw that there are two types of product:
- Tensor Product
- Cartesian Product
Here we are concerned with the Cartesian product, can we extend this concept from graphs to simplexes?
So, for graphs, the tensor product of two edges will be 4 edges like this: So there are:
Since this is a graph there can't be any higher order simplexes. |
|
| If we now move to simplexes, the product of two edges is again a square, but this time its a filled-in square. We can construct this by joining two triangles. Note: we need to reverse the direction of the second triangle so the internal edges cancel out. |
Question: What would be the tensor product of two edges for simplexes?
Now, for each of the triangles in the previous case we will multiply by an edge. Then each of those tables produce a wedge shape which can be made up of 3 tetrahedron shapes: These tetrahedrons can be determined by the order of their edges
|
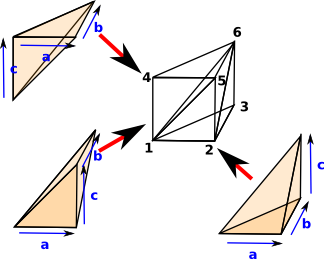 |
We need to determine the order of these tetrahedrons. If any two tetrahedrons have an internal face in common then the tetrahedrons need to be wound in opposite directions so that the internal face cancels out.
In the above example, the tetrahedron (a,c,b) has one face in common with (a,b,c) and another in common with (c,a,b) so if we invert this the internal boundaries will cancel out. So the faces we want are:
- (a,b,c)
- - (a,c,b)
- (c,a,b)
In terms of the vertex numbers shown on the diagram then, if we multiply the triangle (1,2,3) by the edge (1,4), we get:
- (1,2,3,6)
- - (1,2,5,6)
- (1,4,5,6)
This suggests that, if the resulting facets are ordered numerically, then the orientation alternates.
| Going back to graphs here is the product of two triangles: | 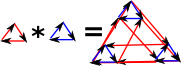 |
So in the simplex case it is filled in and we get a torus. Or do we? If we multiply a 2 dimensional surface by another 2 dimensional surface don't we get a 4 dimensional face? However if we multiply triangle boundaries (non-filled-in triangles) then we get a torus surface. |
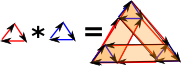 |
More about topology of torus on page here.
Simplexes as a Combinatorics Structure
Returns list, each entry is a 'lattice path' from (0,0) to (x,y) where x is number of entries in sa and y is number of entries in sb.
Calculation of 'lattice paths' is a combinatorics problem so its should really be done by combinatorics code.
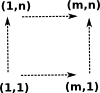 |
The product is represented by a list of simplexes represented by all possible paths from the bottom left (1,1) to the top right (m,n). | |
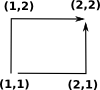 |
So the product of two line segments (1-simplex) is two paths. Each path has 3 points so we interpret this as two triangles: [[[1,1], [1,2], [2,2]],[[1,1], [2,1], [2,2]]] |
 |
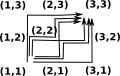 |
The product of two triangle segments (2-simplex) is 6 paths. Each path has 4 points so we interpret this as 6 tetrahedrons: | 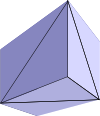 |
FriCAS Code
| First we will calculate the product of two individual orientedFacets. If the inputs are lines then the output is two triangles: | (1) -> A := orientedFacet(1,[1,2])$OrientedFacet
(1) (1,2)
Type: OrientedFacet
(2) -> B := orientedFacet(1,[1,2])$OrientedFacet
(2) (1,2)
Type: OrientedFacet
(3) -> product(A,B)
(3) [([1,1],[1,2],[2,2]),([1,1],[2,1],[2,2])]
Type: List(ProductFacet) |
This result agrees with above theory.
Now a triangle times an edge:
| First we will calculate the product of two individual orientedFacets. If the inputs are lines then the output is two triangles: | (4) -> C := orientedFacet(1,[1,2,3])$OrientedFacet
(4) (1,2,3)
Type: OrientedFacet
(5) -> D := orientedFacet(1,[1,2])$OrientedFacet
(5) (1,2)
Type: OrientedFacet
(6) -> product(C,D)
(6)
[([1,1],[1,2],[2,2],[3,2]), ([1,1],[2,1],[2,2],[3,2]),
([1,1],[2,1],[3,1],[3,2])]
Type: List(ProductFacet) |
This result agrees with above theory.
| If the inputs are solid triangles then the output is:
There are 6 paths through the lattice as expected. |
(7) -> E := orientedFacet(1,[1,2,3])$OrientedFacet
(7) (1,2,3)
Type: OrientedFacet
(8) -> F := orientedFacet(1,[1,2,3])$OrientedFacet
(8) (1,2,3)
Type: OrientedFacet
(9) -> product(E,F)
(9)
[([1,1],[1,2],[1,3],[2,3],[3,3]), ([1,1],[1,2],[2,2],[2,3],[3,3]),
([1,1],[1,2],[2,2],[3,2],[3,3]), ([1,1],[2,1],[2,2],[2,3],[3,3]),
([1,1],[2,1],[2,2],[3,2],[3,3]), ([1,1],[2,1],[3,1],[3,2],[3,3])]
Type: List(ProductFacet) |
Multiplying Complete Simplicial Complexes
Upto now we have only multiplied individual facets but now we need to multiply complete simplicial complexes. This works in a similar way to the Cartesian products of graphs, that is the vertices are the Cartesian set product.
So, first the simplest case I can think of, where the facets are not connected. (a+b)*(x+y) = a*x + a*y + b*x + b*y |
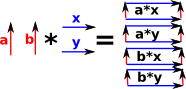 |
| and here the lines have a vertex in common. | 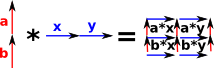 |
So the edges are combined using the usual distributive law but the tricky bit is relating this back to the vertices.
FriCAS Code
Here is the FriCAS Code for products on complete simplicial complexes:
This is not yet working correctly because the orientations are not yet set correctly.
| First we will multiply two edges: | (10) -> ASIMP := FiniteSimplicialComplex(Integer)
(10) FiniteSimplicialComplex(Integer)
Type: Type
(11) -> v1:List(List(NNI)) := [[1,2]]
(11) [[1,2]]
Type: List(List(NonNegativeInteger))
(12) -> vs1:List(Integer) := [1]
(12) [1]
Type: List(Integer)
(13) -> G := simplicialComplex(vs1,v1)$ASIMP
(13) points 1..2
(1,2)
Type: FiniteSimplicialComplex(Integer)
(14) -> product(G,G)
(14) points 1..4
(1,2,4)
(1,3,4)
Type: FiniteSimplicialComplex(Integer)
|
We want the common edge to cancel out and to do this the orientation of the second triangle needs to be negative.
Now multiply two triangles: This gives a torus:
|
(15) -> FACTORY := SimplicialComplexFactory(Integer)
(15) SimplicialComplexFactory(Integer)
Type: Type
(16) -> I := sphereSurface(2)$FACTORY
(16) points 1..3
(1,2)
-(1,3)
(2,3)
Type: FiniteSimplicialComplex(Integer)
(17) -> J := sphereSurface(2)$FACTORY
(17) points 1..3
(1,2)
-(1,3)
(2,3)
Type: FiniteSimplicialComplex(Integer)
(18) -> product(I,J)
(18) points 1..9
(1,2,5)
(1,4,5)
(1,3,6)
(1,4,6)
(2,3,6)
(2,5,6)
(1,2,8)
(1,7,8)
(1,3,9)
(1,7,9)
(2,3,9)
(2,8,9)
(4,5,8)
(4,7,8)
(4,6,9)
(4,7,9)
(5,6,9)
(5,8,9)
Type: FiniteSimplicialComplex(Integer) |
More Information
For more details of the theory of simplex products see this page.
More about topology of torus on page here.
I have put the FriCAS computer code here.