In the geometric form each vertex has a cartesian coordinate instead of a symbol or an index.
In this form we have additional constraints on what makes a valid simplicial complex, the faces are not allowed to overlap.
In 1 Dimension
| Not valid simplicial complex | Convert to simplicial complex | |
|---|---|---|
| These lines overlap so they do not form a valid simplicial complex. We can detect this because line 'A' has an endpoint inside line 'B' and line 'B' has an endpoint inside line 'A' | ||
| It is not always the case that each line has an endpoint inside the other. In this example line 'A' does not have an endpoint inside line 'B' and line 'B' has two endpoints inside line 'A'. So we have to check every endpoint and every line to see if the endpoint is inside the line. |
So when we are testing for an invalid overlap, we need to check each line segment that make up the triangles, if two line segments overlap then we have a non-valid case.
In 2 Dimensions
| Not valid simplicial complex | Convert to simplicial complex | |
|---|---|---|
| These triangles overlap so they do not form a valid simplicial complex. | 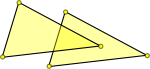 |
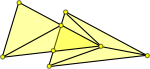 |
| It is not always the case that an overlap will have a vertex inside the triangle. This example is not valid but does not have a vertex inside either triangle. | 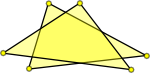 |
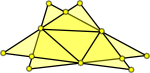 |
So when we are testing for an invalid overlap, we need to check each line segment that make up the triangles, if two line segments overlap then we have a non-valid case.
We can test for overlap of line segments by:
|
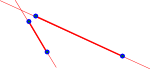 |
Finding the intersection point we need to solve two simultaneous equations.
In 3 Dimensions
| Not valid simplicial complex | |
|---|---|
| This is a lot more difficult, we need to test that no triangles in tetrahedron 'A' pass through the triangles in tetrahedron 'B'. | 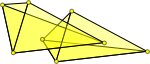 |
There are well known algorithms for determining whether 2 triangles in 3 dimensions intersect. For instance:
- Möller’s algorithm Möller 97 (see http://www.tandfonline.com/doi/abs/10.1080/10867651.2003.10487580)
- Held’s algorithm
more info on site here.
In 'n' Dimensions
Is there a generic test that will work in any number of dimensions?
Optimisation
These checks for overlapping faces could use a lot of CPU time and therefore ways to speed things up could be worthwhile, the following approaches are possible:
Bounding Boxes
It is very simple to generate an 'n' dimensional rectangle (bounding box) around each faces and it is very simple to check these rectangles for overlap. If these bounding boxes do not overlap then the faces inside them cannot overlap. So we can test all combinations of bounding boxes for overlap and then only those that do will require the more expensive (in CPU time) tests.
Moving Line
Rather than test every combination of faces we imagine a line moving across the space and check for overlaps as we go.
|