Join, Star and Link

Join, Star and Link are important operations on simplectical complexes. This page discusses a FriCAS implementation of these.

Join

The code includes a join operation like this: 

simplicialJoin : (a : %, b : %) -> %

The simplectial join of A and B is a simplectical complex with the vertices and simplexes defined as follows:

Vertices

Are disjoint union of vertices of A and vertices of B

vertexSet(simplicialJoin(A,B)) = vertexSet(A)intersectionvertexSet(B)

If A and B have common vertices then the vertices of B will be renamed to make then different from A.

simplexes

A subset of AintersectionB is a simplex of simplicialJoin(A,B) if and only if it is:

Properties of simplicialJoin

May be geometrically thought of as a cone over A with tip of shape B.

simplicialJoin is commutative and associative.

dim(simplicialJoin(A,B)) = dim(A) + dim(B) + 1

Example 1

Here is an example of the join of 2 lines:

[1, 2] and [3, 4]

This gives 4 points and the following simplexes:

  • [1, 2]
  • [3, 4]
  • [1, 2 , 3, 4]
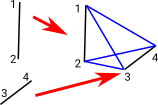 join simplex

but each simplex contains all its sub simplexes so the join is just:

(1, 2, 3, 4)

We can calculate this using FriCAS like this:

Note: the implementation of simplicialJoin refactors the indices of the second operand, if necessary, to make sure the points being joined are disjoint. 

(1) -> line := line()$SimplicialComplexFactory(Integer)

   (1)  points 1..2
           (1,2)
                   Type: FiniteSimplicialComplex(Integer)
(2) -> simplicialJoin(line,line,true)

   (2)  points 1..4
         (1,2,3,4)
                   Type: FiniteSimplicialComplex(Integer)
The above example is just one simplex so here is an example where the operands have multiple simplexes. simplex join

Each operand has two simplexes. The result has all 4 combinations of these simplexes. 

(3) -> ASIMP := FiniteSimplicialComplex(Integer)

   (3)  FiniteSimplicialComplex(Integer)
                                               Type: Type
(4) -> v1:List(List(NNI)) := [[1::NNI,2::NNI],[2::NNI,3::NNI]]

   (4)  [[1,2],[2,3]]
                      Type: List(List(NonNegativeInteger))
(5) -> sc1 := simplicialComplex([],v1)$ASIMP

   (5)  points 1..3
           (1,2)
           (2,3)
                   Type: FiniteSimplicialComplex(Integer)
(6) -> simplicialJoin(sc1,sc1,true)

   (6)  points 1..6
         (1,2,4,5)
         (1,2,5,6)
         (2,3,4,5)
         (2,3,5,6)
                    Type: FiniteSimplicialComplex(Integer)

Star

We can calculate this using FriCAS like this: 

x

 

Link

 

We can calculate this using FriCAS like this: 

x

 

 

metadata block
see also:
  • I have put the code here.
Correspondence about this page

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.