For a long time I have wanted to program a computer algebra system (CAS) using the Scala programming language. However I have never really found a convincing design that would do what I want (A few years ago I previously asked this type of question on forums). Perhaps now the capabilities of Scala have increased, perhaps also my own knowledge has increased, although I am far from being an expert on any of this stuff. Perhaps now might be the time to ask again?
By 'computer algebra system (CAS)' I mean a program that will handle, not just numerical mathematics, but also symbolic algebra, discrete algebra, mathematical logic and so on.
So how do we specify and design such a program? Is there some way to break mathematics down into manageable parts? From what little I know about Gödel's theorems I think we can't derive a canonical way to do this but mathematicians, over the years, have evolved ways to break down the subject.
Universal Algebra
One approach is 'universal algebra'. We can divide the subject into:
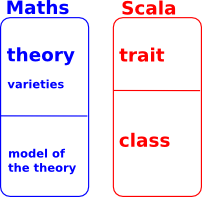
- Theories
- Varieties of those theories
- Models of those theories.
So theories are things like:
- Set theory
- Graph Theory
- Group Theory
- .. and so on.
This links up quite nicely with Scala in that:
- Theories could correspond to traits.
- Models could correspond to classes.
- Varieties could correspond to traits with type parameters
However, they don't quite line up, in particular:
|
 |
Example Vectors
As an example to illustrate this lets look at 'vectors' (the mathematical concept of vector, not what the java class library uses the word for).
trait Field {
def *(a:Field,b:Field)
def +(a:Field,b:Field)
// other methods ommited for this example
}
trait Vector2d[Scaler <: Field] {
def *(a:Scaler,b:Field)
def +(a:Field,b:Field)
// other methods ommited for this example
} |