Maths - decomposition of rotations

This is about how to factor (decompose) a single 3D rotation into two component rotations at right angles to each other. One component is a swing of the direction vector to a new direction and the other component is a twist about the direction vector.

This is potentially useful where we might want to apply constraints to the rotation, for instance a robot arm, there may be a mechanical limitation on the angle through which it will twist.

First I would like to define how we are breaking down this rotation into a set of joints,

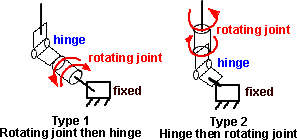
Is it a rotating joint and then a hinge, or is it a hinge and then a rotating joint, or are these two equivalent?

Could we replace either of these by 2 hinges offset from each other? provided that one of them is inline with the hinge of the other.

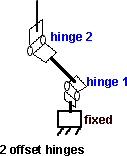
I was originally assuming that swing and twist was represented by type 2 with the swing being represented by the hinge and the twist being represented by the rotating joint, however the revolute joint is shown as type 1.

These joints only have 2 degrees of freedom, so to represent any rotation we need to replace the hinge with a ball and socket joint, or we need to have the rotating joint both before and after the joint. More on joint types here.

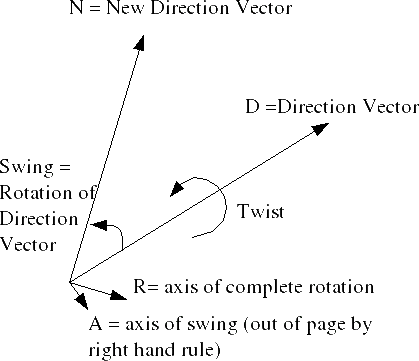
From the diagram above define the following vectors:

D=original vector direction
N=new vector direction
A=axis of swing rotation
R=axis of combined rotation

The twist is around the direction vector, we could apply the twist about D first and then apply the swing, or apply the swing and then twist about N, or even apply the swing and twist simultaneously so if we define the following corresponding quaternions:

QD = twist about D (if twist is done before swing)
QN = twist about N (if twist is done after swing)
QS = swing rotation
QR = complete rotation

So using these definitions:

QR = QS * QD= QN * QS

note: I'm not saying here that the rotation compositions are commutative, all I'm saying is that the rotation could be decomposed into the swing(QS) first and then the twist(QN) or by the twist(QD) first and then the swing(QS). This is not commutative because QD != QN.

derivation of decomposition from minorlogic

Let Us take by Twist quaternion the quaternion of look
Twist ( TR, W )

where
TR = axis of twist rotation
W = combined rotation scalar part of quaternion

TR = axis of twist rotation computed like Projection of

R = axis of combined rotation

to the

D = original vector direction

TR = projection(R, D );

If the

combined_rotation = swing*twist
than
swing = combined_rotation/twist =
swing = combined_rotation*twist.inversed() ;
( or conjugated if the twist is unit quat)

swing = combined_rotation*twist.inversed() ;

combined_rotation have two parts
vector part -> R
and scalar part W

combined_rotation( R, W)

twist represented as

twist(TR, W)
and twist conjugatad as twist( -TR, W)

than swing rotation can be calculated by quaternion multiplication rule

q*q' = q( cross(v,v') + wv' + w'v, ww' - dot(v,v') )

as

combined_rotation( R, W) * twist( -TR, W) =

swing( cross(R, -TR) + R*W - TR * W, W*W - dot(R, -TR) ) =
swing( cross(R, -TR) + W*(R - TR), W*W - dot(R, -TR) )

The vector cross(R, -TR) perpendicular to the D because -TR lay on the "D", and W*(R - TR) perpendicular because:

W*( R - TR ) -> is a W*( R - projection (R, D )) ->

is a W*( perpendicular_component(R, D )) ;

The sum of two perpendicular to D vectors give the vector that is perprndicular to D too, because thay lay in one plane , and tham composition lay in that plane.

because of swing was computed as

swing = combined_rotation*twist.inversed() ;

their composition

combined_rotation = swing*twist;

And we know their properties that Twist rotate only about D vector and Swing only about vector that is parallel to D.

It all work in the Pure rotation , when D represent the direction in LOCAL object orientation frame.

So if we have the Rotation R1 and R2 , and want to find Swing and Twist from R1 to R2 about any Direction vector. We need to made such :

find the delta rotation such that

R2 = R1 * Delta_Rotation

Delta_Rotation = R2/R1

Than decompose the Delta_Rotation by Direction Vector in the Delta_Rotation Frame.

More info can be found in Shoemake "Fiber bundle twist reduction" or in it's tutorial.

There he finf the Swing rotation first , by finding "shortest arc" between

Direction Vector
and
New Direction Vector

And than find the Twist.

Example

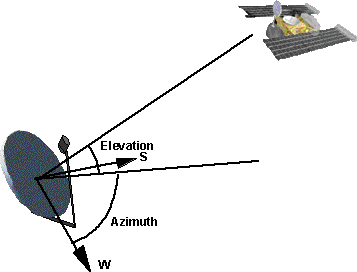
Here is an example to illustrate swing & twist, aiming the dish (elevation & azimuth) is the swing, and the polarisation of the signal (vertical or horizontal) is the twist.

example

metadata block

see also:
Correspondence about this page	Forum Discussion
Book Shop - Further reading. Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.	Graphics Gems - Lots of useful algorithms and snippets of theory - These are reference books rather than books you read from cover to cover. If you can afford it they are worth having on the shelf (I wish I could!) They might just solve a problem which could otherwise take days to work out. Graphics Gems II Graphic Gems III: IBM Version (with diskette) Graphics Gems IV: IBM Version (with Diskette) Graphics Gems V: IBM Version (with disk) Other Math Books

Maths - Decomposition of rotations.

derivation of decomposition from minorlogic

Example

EuclideanSpace

Direction vs. Rotation

Successive Rotations

Example Dish Example