Definition of terms:

• Euler Angles
• Matrix

This depends on what conventions are used for the Euler Angles. The following are derived on the euler angle page, the first assumes NASA Standard Airplane:

[R] =

c θ *c φ -c θ *s φ s θ cψ*sφ + s ψ* s θ*c φ cψ*cφ -s ψ*s θ*s φ -s ψ*c θ sψ*sφ - c ψ* s θ*c φ sψ*cφ + c ψ*s θ*s φ c ψ*c θ

 

Or, from the same page, this uses NASA Standard Airplane taking angles in the reverse order:

[R] =

c ψ*c θ sψ*cφ + c ψ*s θ*s φ sψ*sφ - c ψ* s θ*c φ -s ψ*c θ cψ*cφ -s ψ*s θ*s φ cψ*sφ + s ψ* s θ*c φ s θ -c θ *s φ c θ *c φ

 

Java code to do conversion:

/** this conversion uses NASA standard aeroplane conventions as described on page:
*   http://www.euclideanspace.com/maths/geometry/rotations/euler/index.htm
*   Coordinate System: right hand
*   Positive angle: right hand
*   Order of euler angles: [R3][R2][R1] = [about z][about y][about x] = [bank][attitude][heading]
*   matrix row column ordering:
*   [m00 m01 m02]
*   [m10 m11 m12]
*   [m20 m21 m22]*/
public final void rotate(double heading, double attitude, double bank) {
    // Assuming the angles are in radians.
    double c1 = Math.cos(heading);
    double s1 = Math.sin(heading);
    double c2 = Math.cos(attitude);
    double s2 = Math.sin(attitude);
    double c3 = Math.cos(bank);
    double s3 = Math.sin(bank);

    m00 = c1 * c2;
    m01 = -s1 * c2;
    m02 = s2;
    m10 = s1 * c3+(c1 * s2 * s3);
    m11 = (c1*c3) - (s1 * s2 * s3);
    m12 = -c2 * s3;
    m20 = (s1 * s3) - (c1 * s2 * c3);
    m21 = (c1 * s3) + (s1 * s2 * c3);
    m22 = c2*c3;
}

Example

we take the 90 degree rotation from this:

to this: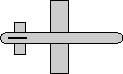

As shown here the axis angle for this rotation is:

heading = 0 degrees
bank = 90 degrees
attitude = 0 degrees

so substituteing this in the above formula gives:

• c θ =cos(heading) = 1
• c φ =cos(attitude) = 1
• cψ =cos(bank) = 0
• s θ = sin(heading) = 0
• s φ =sin(attitude) = 0
• s ψ =sin(bank) = 1

[R] =

c θ *c φ -c θ *s φ s θ cψ*sφ + s ψ* s θ*c φ cψ*cφ -s ψ*s θ*s φ -s ψ*c θ sψ*sφ - c ψ* s θ*c φ sψ*cφ + c ψ*s θ*s φ c ψ*c θ

[R] =

1 0 0 0 0 -1 0 1 0

This agrees with the matix rotations here.

other examples in 90 degree steps are shown here.