The concept of 'spin' is important for quantum mechanics. It contributes to the angular momentum that we experience in classical mechanics but it has strange properties, for instance, a rotation of 360° inverts it and it does not return to its original value until it has rotated 720° (see quaternions).
It seems to me that this property of particles can be explained by applying the relativity postulates to particles rotating very quickly. However this idea seems to be controversial, for example there we a series of papers in The British Journal for the Philosophy of Science:
| "On the Origin of Spin in Relativity" The British Journal for the Philosophy of Science, Vol. 40, No. 3. (Sept 1989),pp. 409-412 |
Here are some papers and books which show the controversy and explain the issues.
At the moment I don't have the expertise to validate the derivation of spin using relativity concepts, the best I can do at the here is an intuitive (non rigorous) justification. I am still working on it so hopefully I will soon understand it better. Personally I hope it does work out because this way of looking at it has given me a way to answer questions that had me confused before, like:
- Why does spin, which is a continuous rotation, have the properties of a finite rotation?
There are some things this does not appear to explain such as quantization.
Intuitive (non rigorous) justification
Imagine that we have a spinning disk and we are looking at it along its axis of rotation. Imagine that it is rotating very fast so that its rim is traveling at the speed of light:
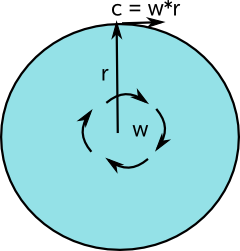
Where:
- c = speed of light = speed at outer rim.
- r = radius of disk
- ω = angular velocity
Now imaging that the frame in which the disk exists starts rotating relative to the observer at a rate of Δω so that the disk appears to be rotating at an angular velocity of ω+Δω.
Now according to SR we must still see the outer disk traveling at the speed of light and so at the rim the disk will appear to be rotating at ω but toward the hub the speed is much lower and so the angular velocity is ω+Δω. So the disk appears to be rotating at different angular velocities at different radii.
Because the velocity is perpendicular to the viewer the distance extension is zero but the time dilation is:
t0= tv / √(1 - (v/c)2)
we can express v and c in terms of r
c=ω*rrim
v=ω*r
which gives the time dilation in terms of radius:
t0= tv / √(1 - (r/rrim)2)
so at the rim time would not appear to be progressing at all whereas, at the hub, time would be progressing at the normal rate.
What would happen if the disk were to collapse inward to approach a single point or singularity - like a mini black hole? Assuming that it still retained its angular momentum then:
We take the limit as r -> 0 then we get ω -> ∞.
I don't know of any rule which gives an upper limit to ω provided that v does not exceed c.
So what would be the time dilation of the singularity? Would it be an average between the rim where time would not appear to be progressing at all and the hub there time would be progressing at the normal rate. This would mean, for such a singularity time would progress at half the rate to the outside observer?
Can this be related to the way that, for certain types of particle, spin does not return to original until it rotates through 720° ?
History
papers and books which show some of the history.
Note: near the top of p. 29 of Hestenes' Oersted Lecture, Hestenes claims to have heard the idea via Feynman although Hestenes seems to lead the non-relativistic view.


