Adding complex numbers
Just add the real and imaginary components independently as follows:
(a + i b)+(c + i d) = (a+c) + i (b+d)
Multiplying complex numbers
To multiply just expand out the terms and group as follows:
(a + i b)*(c + i d) = (a*c - b*d) + i (a*d + b*c)
I don't know if multiplications are so costly in CPU time in modern computers, but if we do want to minimise multiplications we can do a complex multiplication using 3 floating point multiplications as follows:
multiply(other){
double t1= a * other.a;
double t2= b * other.b;
double t3= (a + b)*(other.a+other.b);
a = t1 - t2;
b = t3 - t1 - t2;
}
Norm
This is the distance (r) of a + i b from the origin.
It is written as:
r = | a + i b |
by pythagorous:
r = | a + i b | = math.sqrt(a*a + b*b)
Check that:
|a + i b|*|c + i d| = |a*c - b*d + i (a*d + b*c)|
Division
We don't tend to use the 
notation for division, since complex multiplication is not commutative we need
to be able to distinguish between [a][b]-1 and [b]-1[a].
So instead of a divide operation we tend to multiply by the inverse.
In order to calculate the inverse 1/b we multiply top and bottom by its conjugate as follows, conj(b)/b*conj(b). Multiplying a complex number by its conjugate gives a real number and we already know how to divide by a real number.
The conjugate of a + i b is a - i b
so (a + i b)*conj(a + i b) = a*a + b*b
so 1/(a + i b) = a/(a*a + b*b) - i b/(a*a + b*b)
Representing Rotations using complex numbers
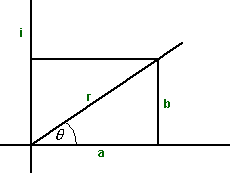
instead of a + i b the complex number could also be represented in what is known as the polar form:
r (cos(θ) + i sin(θ))
in other words replace:
- a = r cos(θ)
- b =r sin(θ)
we can use ei θ = cos(θ) + i sin(θ) to give the exponential form:
r ei θ
If we want combine the result of two rotations, for example rotate by θ1 then rotate by θ2, then we multiply the corresponding complex numbers because:
ei (θ1+θ2) = ei θ1 * ei θ2
Or to combine two rotations by addition if we add the logarithms of the complex numbers.
Complex Number Calculator
The following calculator allows you to calculate complex arithmetic. Enter the values into the top two complex numbers and then press "+ - or * " to display the result in the bottom number:
