Here we look at structures where some part, or parts, of it also have the same structure. This is discussed on the page about sub-objects here.
For an endofunction a fixpoint is certain value or values that map to themselves. This concept is useful in mathematics generally and also in computing for the study of recursive type definitions. |
Example 1 - Real Numbers
 |
Given an endofunction from the reals to itself. There may be some point on the line that the endofunction will map to themselves. Some of those fixpoints may be attractors and some may be repellers. That is, if we choose a non-fixpoint and continuously apply the endofunctor, then the resulting point may move towards or away from the fixpoints. |
Brouwer's fixed-point theorem
For any continuous function f with certain properties mapping a compact convex set into itself there is a point x0 such that f(x0) = x0.
- Example of convex set - triangle
- Compact means - closed and bounded.
Can be proved using Sperner's Lemma.
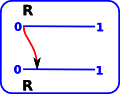
Here is an outline of an intuitive 'proof' for a mapping on the reals from 0 to 1. We will try to avoid a fixpoint to see how it is forced on us. Starting with the point at '0', we cant map it to '0' or that would be a fixpoint, so it must map to some point greater than '0'. |
 |
| Again with the point '1', since we are trying to avoid a fixpoint, we must map to some point less than '1'. | 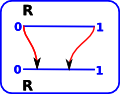 |
| Now we fill in the gaps. Since the mapping is continuous and '0' is increasing and '1' is decreasing, there must be some point in between that is fixed. There could be more than one fixpoint but there must be an odd number. | 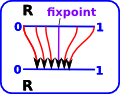 |
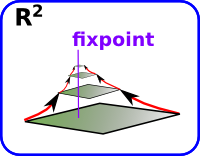
We can extend this from the reals R to Rn. For instance, a classic example in R2 is a map. If a map is held over the land that it represents then there will always be at least one point on the map that is directly over the point that it represents.
RecursionRecursion is related to fixpoints. We can extend the map example above. If the map is so accurate that it shows itself on the map, then we have a form of recursion, with the map showing a map which shows an even smaller map and so on. Then there will be a fixpoint that goes through the same point on all the maps. |
 |
Example 2 - Finite Sets
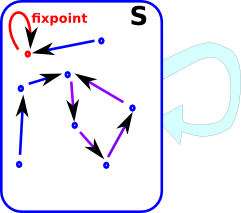 |
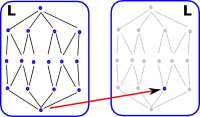
Here is an example of a fixpoint for a finite set. I have drawn the arrows representing the endofunction internally. That is, not going out round the light blue arrow, this makes the diagram less cluttered although we may think of the endofunction as being external. The red dot is a fixpoint, so we can apply the endofunction as many times as we like, it will always map to itself. For a finite set, like this, following the arrows (applying endofunction repeatedly) will always lead us to a fixpoint or a loop. |
Example 3 - Lattice
In a similar way to Brouwer's theorem above, we will try to construct a lattice endofunctor without fixpoints (to show that it can't be done). We will start with bottom, since we are trying to avoid fixpoints this must map to a different point. |
|
| Similarly with top. | 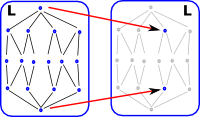 |
We must now map all the other nodes, in a way that respects the meet and join structure. This does have a fixpoint as marked. |
 |
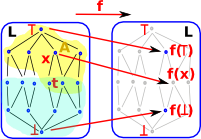
Knaster-Tarski theorem
If L is a complete lattice, then every monotone (i.e., order-preserving) map
f : L -> L has a fixed point
and the fixed points of f form a complete lattice.
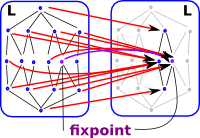
On the diagram (right), the nodes with a yellow background map to values with a lower or equal value (f(x)≤x), the nodes with a blue background map to values with a greater or equal value (x≤f(x)). The intersection of this (green background) have both f(x)≤x and x≤f(x) that is x=f(x). In other words this is the fixpoint. This works because:
|
 |
| Imagine that, for a given edge, the highest node increased and the lowest node decreased. Then we would end up with intermediate nodes that are not in the codomain. | 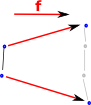 |
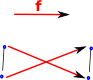
Imagine that, for a given edge, the lowest node increased and the highest node decreased. Then f would not be monotone. Therefore there must be fixpoints inbetween. |
 |
These fixed points form a complete lattice because if 'x' is a fixpoint and 'y' is a fixpoint then 'x/\y' is a fixpoint and 'x\/y' is a fixpoint.
For more discussion about mappings between lattices see page here.
Example 4 - Inductive Partial Order
Pataraia’s theorem
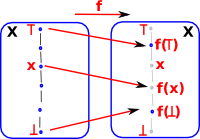
If L is an inductive partial order (ipo), then every monotone map f:L->L has a (least) fixed point.
Definition of ipo - A poset with a bottom element and joins of directed subsets
(related concept - An inductive poset is a poset in which every chain has an upper bound. )
Partially Ordered Sets
Bourbaki–Witt theorem
if X is a non-empty chain complete poset, and
f : X->X
such that
![]() x. f(x) ≥ x
x. f(x) ≥ x
then f has a fixed point.
Such a function f is called inflationary or progressive.
The proof is similar to Knaster-Tarski above.
|
 |
| Imagine that, for a given edge, the highest node increased and the lowest node decreased. Then we would end up with intermediate nodes that are not in the codomain. |  |
Imagine that, for a given edge, the lowest node increased and the highest node decreased. Then f would not be monotone. Therefore there must be fixpoints inbetween. |
 |
Initial Algebra
 |
An Initial Algebra is a fixpoint (Lambek’s theorem) F A |
Kleene's recursion theorems
- Rogers' fixed-point theorem. If F is (total) computable, it has a fixed point.
- For any partial recursive function Q(x,y) there is an index p such that:
φp λ y.Q(p,y).
λ y.Q(p,y).
Quine
A quine is a computer program which takes no input and produces a copy of its own source code as its only output.
A quine is a fixed point of an execution environment, when the execution environment is viewed as a function