Iterating Functions
Imagine it we take the output of a function and feed it back to the input then we can keep applying the function repeatedly. At first this may seem a strange thing to do but we often need to do this sort of thing when we are modeling the real world. For instance, if we are modeling the motion of an object in a force field or the behavior of a weather system, we can feed in the input state and then use the function to calculate the state at time t+Δt we can the feed this new state into the function to simulate its behavior.
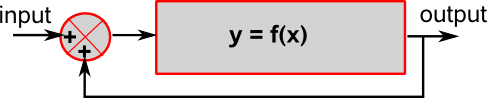
This operation may, or may not, be stable. The output may tend to zero, or to a given value, or to infinity, or it may fluctuate in a chaotic way.
Often real world functions will have 'memory' such as storage of momentum or thermal energy which can be represented as integration. This may make the output more stable but even so weather systems and multi-body orbits can be very unstable.
(see Range Kutta Integration and numerical methods)
Strange Attractors
If the output is multi-dimensional, for example represented by a point in a complex plane, then we can track its path over many iterations. Sometimes the point will spiral round and tend towards a point: called a sink. Alternatively other points may always produce paths that diverge from them: called a source.
So effectively the whole of the two dimensional plane is made up of a set of lines (which never cross) going from sources to sinks.
Mandelbrot Set
The iterative function is:
zn+1 = zn2 + c
Where:
- zn = a complex number at step n
- c = a complex number constant
If :
z0 = 1 and c=0 the value of zn remains at 1
z0 < 1 and c=0 the value of zn will approach 0 as n approaches ∞
z0 > 1 and c=0 the value of znwill approach ∞ as n approaches ∞
However if z0 is complex then the value of zn is chaotic and difficult to predict.
So if we plot z0 on a plane and assign colours to each pixel depending on how quickly zn approaches ∞ (or does not) then we get a fractal image.
Julia Sets


