When we are using a monad in a Haskell program we can take some function of a type 'a':
f :: a -> a
and add some 'effect' to that function:
a -> m a
This effect could be somthing like input/output or state which would otherwise make the program non-pure functional.
Identity Monad
On this page we will create instances of the built in Monad class, which is defined in the prelude like this:
class Monad m where return :: a -> m a (>>=) :: m a -> (a -> m b) -> m b |
In the identity monad the modad does not have any additional effect and the function 'f' is applied directly to x:
module Main where
instance Monad Ident where
return x = x
x >>= f = f x
|
Maybe Monad
| We can introduce a functor which takes any type and adds a 'nothing' value. | 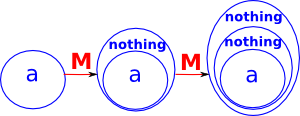 |
| We can draw this as an endo-functor. | 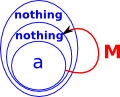 |
Maybe - Natural Transformations
| The unit transform adds the 'nothing' value to type 'a' | 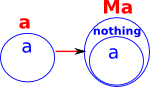 |
| The mult transform combines the inner and outer 'nothing' into a single nothing. | 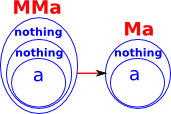 |
Maybe - Haskell Code
module Main where
instance Monad Maybe where
return x = Just x
(Just x) >>= f = f x
Nothing >>= _ = Nothing
(Just _ ) >> f = f
Nothing >> _ = Nothing
Fail _ = Nothing
maybe :: b -> (a -> b) -> Maybe a -> b
maybe n _ Nothing = n
maybe _ f (Just x) = f x |