There are at least two approaches to algebra in category theory:
- Monads and algebras
- Lawvere algebraic theories
The relationship between algebras and monads is discussed on the page here. On the remainder of this page we discuss Lawvere algebraic theories.
Lawvere Algebraic Theories
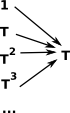 |
In this approach, instead of using signatures as we would in universal algebra, we define arrows from powers of our structure 'T'. This means that we can only define algebras on a structure with associative products. |
| We can then use this to define the axioms like this: | 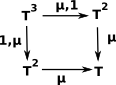 |
Models of Algebraic Theories
See page here for a general discussion of algebraic theories and models of those theories.
A model of the theory 'T' is a functor F: T->Set which preserves finite products.
Initial and Final Algebras
Category Theory and W-types
W-types are initial algebras for polynomial endofunctors.