Vector Calculus is often used to analyse the movement of fluids, but there is no reason why we should not use it to analyse solid objects, provided that we apply it to regons of space where the vector field is continous..
If we take a velocity field of a rotating object we might get a field that looks like this:
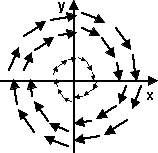
If we take the curl of this field we would get a different vector field
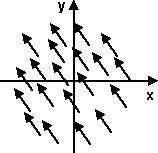
To see how this relates to the angular velocity (
)
we can calculate curl as follows, if the following diagram shows the velocity
of a point on a solid object rotating about the origin:
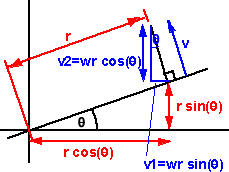
v1 = component of v in x dimention = -v sin(θ)
= -wr sin(θ)
v2 = component of v in y dimention = v cos(θ)
= wr cos(θ)
v3 = component of v in z dimention = 0
x = r cos(θ)
y = r sin(θ)
z = 0
dv1/dy = d(-wr sin(θ)/d(r
sin(θ)) = -w
dv1/dz = 0 /* because the object boes not change in the z direction
*/
dv2/dx = d(wr cos(θ)/d(r
cos(θ)) = w
dv2/dz = 0
dv3/dx = 0 /* because there is no component of velocity in the z
direction */
dv3/dy = 0
so:
curl(
)
= (d v3 / dy - d v2 / dz)i + (d v1 / dz - d
v3 / dx)j + (d v2 / dx - d v1 / dy)k
= 0 i + 0 j + (w + w) k
= 2w k
Therefore curl of a solid object is 2w along the line of the axis of rotation.
