The ordering of vertices (0-simplicies) gives a direction to edges (1-simplicies). It also allows a 2-simplex to represent the composition of two edges. see simplicial sets on this page. |
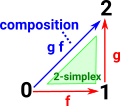 |
So if these two edges (f and g) are given then we have a unique composition (if we are working with categories), call it 'h', which is g f (we say g after f).
But what if one of the other edges is the unknown? We may sometimes be able to construct it although sometimes it may not exist and sometimes it may not be unique (multiple possibilities).
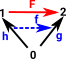 |
If we fix F then given h we can construct g but we may not be able to construct g from h. It gives rise to a higher order morphism f. here f goes in the same direction as F so it is covariant. |
| In this case we also fix F but this time h and g go away from it, then given g we can construct f. Again it gives rise to a higher order morphism f. now f goes in the opposite direction as F so it is contravariant. |  |
2-Simplcies over Sets
As a specific example lets start working over sets. That is, nodes are sets, edges are maps between sets and 2-simplcies are compositions of these maps.
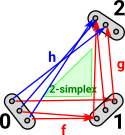
Here is an example looking inside the sets and mappings: The mappings commute in that we get to the same element if we go via h or go via f and then g. That is, given f and g we can uniquely construct h. |
 |
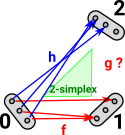 |
Can we do this for other edges? In this case given f and h can we construct g? In this case we can, in fact there are multiple possibilities so there is no unique solution. In other cases there may not be any solutions which commute. |
So how can we better characterise this situation?
| One approach might be to use the property that a function can be decomposed into injective and surjective functions. If we go surjective and then injective (bottom route on diagram) then there is one unique way to do this. If we go injective and then surjective (top route on diagram) then there are many ways to do this.
|
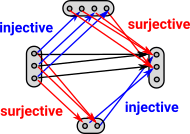 |
monic (monomorphism) fg = fh implies g = h |
In category theory terms we are decomposing into monic and epic morphisms (see page here). |
epi (epimorphism) if = jf implies i = j |