Simplicial Sets - Sage Code

Sage is mathematical software, it implements simplicial sets as follows:

Sage Code:

• Sage simplicial sets code - topology - definition of AbstractSimplex
  • SimplicialSet_arbitrary at 1095
  • SimplicialSet_finite at 3113

AbstractSimplex AbstractSimplex represents one simplex where the vertices are numbered sequentially from 1 unless there are degeneracies specified.

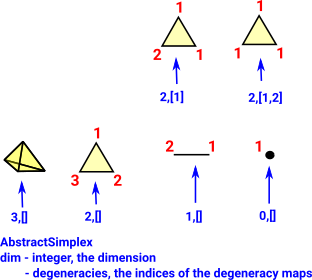SimplicialSet

sage: from sage.topology.simplicial_set import AbstractSimplex, SimplicialSet
            sage: v = AbstractSimplex(0)
            sage: w = AbstractSimplex(0)
            sage: e = AbstractSimplex(1)
            sage: X = SimplicialSet({e: (v, v)})
            sage: Y = SimplicialSet({e: (w, w)})

This is a hierarchy: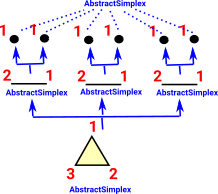

SimplicialSet_finite inherits from SimplicialSet_arbitrary and GenericCellComplex

SimplicialSet_arbitrary inherits from Parent which makes them containers.

Product

One way to do this is find all combinations and then filter out those that are not correctly ordered.

product(A, B) returns the same as ((x,y) for x in A for y in B).

see Python code here.

We can extend this from a product to a pullback with further filtering.

Other Sage Code

• Sage simplicial sets documentation
• Sage simplicial sets code - category - definition of SimplicialSets
• Sage simplicial sets code - homology
• Sage simplicial sets code - topology - examples
• Sage simplicial sets code - topology - morphisms and homsets of simplicial sets

 

EuclideanSpace

home