Nerve in Category TheoryInternal categories can be described by diagrams within an ambient category. The sequences of composable arrows constitute the nerve of the category which is a simplicial set. (see Saunders Mac Lane, Categories for the Working Mathematician p267). The nerve N(C) of a small category C is a simplicial set constructed from the objects and morphisms of C. The geometric realization of this simplicial set is a topological space, called the classifying space of the category C. These closely related objects can provide information about some familiar and useful categories using algebraic topology, most often homotopy theory. see Wiki. The nerve defines a functor N: C -> Hom(Δop ,set) It has a left adjoint |-|:Set Δop -> C called realisation. The realization operation is the left Kan extension of SC :S->C along the Yoneda embedding S->[Sop,V] (i.e. the Yoneda extension) see ncat .
|
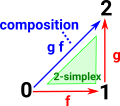
The ordering of vertices (0-simplicies) gives a direction to edges (1-simplicies). It also allows a 2-simplex to represent the composition of two edges. For more about this see this page . |
 |
Generating Nerve
 |
As an example start with a complex containing two triangles and two lines. | {a,b,c} {b,c,d} {a,e} {d,e} |
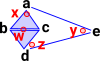 |
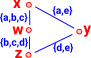
Then write down all the intersections. For complexes these intersections are the common faces which now become the points in the diagram. | w := {b,c} x:={a} y:={e} z:={d} |
 |
Then connect these points if they were connected before. |