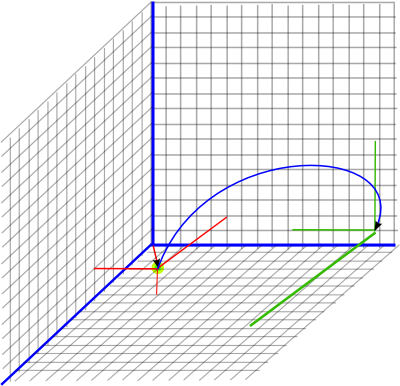
Since conformal space is 2 dimensions higher than the space we are working in, that means to model 3D Euclidean space, we need 5D Conformal space.
Example
So if we are initially at point (x=3, y=4, z=5) this will be represented by the multivector:
P1 = -n0+ 50 n∞ + 6 n1 + 8 n2 + 10 n3
A pure displacement of (x=4, y=2, z=6) will be represented by the multivector:
1 + 2 n∞1 + 1 n∞2+ 3 n∞3
So to combine these, to give the resulting position, we use P2 = m * P1 * m' to give:
p2 = (1 + 2 n∞1 + 1 n∞2+ 3 n∞3)*(-n0+ 50 n∞ + 6 n1 + 8 n2 + 10 n3)*(1 - 2 n∞1 - 1 n∞2- 3 n∞3)
multiplying out the first two terms using the above multiplication table we get (using the rules explained on this page):
P2 = (-n0+ 50 n∞ + 3 n1 + 4 n2 + 5 n3
-4n∞1n0+ 200 n∞1n∞ + 12 n∞1n1 + 16 n∞1n2 + 20 n∞1n3
-2n∞2n0+ 100 n∞2n∞ + 6 n∞2n1 + 8 n∞2n2 + 10 n∞2n3
-6n∞3n0+ 300 n∞3n∞ + 18 n∞3n1 + 24 n∞3n2 + 30 n∞3n3)*(1 - 4 n∞1 - 2 n∞2- 6 n∞3)
P2 = (-n0+ 50 n∞ + 3 n1 + 4 n2 + 5 n3
+4n∞01+ 12 n∞+ 16 n∞12 - 20 n∞31
+2n∞02- 6 n∞12+ 8 n∞+ 10 n∞23
+6n∞03+ 18 n∞31 - 24 n∞23+ 30 n∞)*(1 - 4 n∞1 - 2 n∞2- 6 n∞3)
P2 = (-n0+ (50+12+8+30) n∞ + 3 n1 + 4 n2 + 5 n3
+4(n1-n0∞1) + (16-6) n∞12 +(18- 20) n∞31 +2(n2-n0∞2) + (10-24) n∞23
+6(n3-n0∞3))*(1 - 4 n∞1 - 2 n∞2- 6 n∞3)
P2 = (-n0+100n∞+7n1+6n2+11 n3-4 n0∞1-2 n0∞2-6 n0∞3+10 n∞12-2 n∞31-14 n∞23
)*(1 - 4 n∞1 - 2 n∞2- 6 n∞3)
P2 = -n0+100n∞+7n1+6n2+11 n3-4 n0∞1-2 n0∞2-6 n0∞3+10 n∞12-2 n∞31-14 n∞23
+4n0n∞1-400n∞n∞1-28n1n∞1-24n2n∞1-44 n3n∞1+16 n0∞1n∞1+8 n0∞2n∞1+24 n0∞3n∞1-40 n∞12n∞1+8 n∞31n∞1+56 n∞23n∞1
+2n0n∞2-200n∞n∞2-14n1n∞2-12n2n∞2-22 n3n∞2+8 n0∞1n∞2+4 n0∞2n∞2+12 n0∞3n∞2-20 n∞12n∞2+4 n∞31n∞2+28 n∞23n∞2
+6n0n∞3-600n∞n∞3-42n1n∞3-36n2n∞3-66 n3n∞3+24 n0∞1n∞3+12 n0∞2n∞3+36 n0∞3n∞3-60 n∞12n∞3+12 n∞31n∞3+72 n∞23n∞3
P2 = -n0+(100+66+28+12)n∞+7n1+6n2+11n3+(-4+4) n0∞1+(2-2) n0∞2+(6-6)n0∞3+(10-24+14) n∞12+(44-2-42) n∞31(36-14-22) n∞23
P2 = -n0+206 n∞+7 n1+6 n2+11 n3
Pure Rotation (no displacement)
If the displacement is zero then n1,n2,n3 = 0 and the rotation is represented by the multivector: cos(θ/2) + axsin(θ/2) n23 + aysin(θ/2) n31 + azsin(θ/2) n12
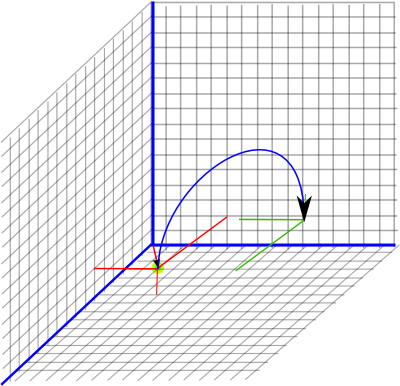
Example
Applying a rotation of point (3,4,5) by 180° around the x axis is given by:
P2 = (n23)*(-n0+ 50 n∞ + 6 n1 + 8 n2 + 10 n3)*(-n23)
P2 = (-n23n0+ 50 n23n∞ + 6 n23n1 + 8 n23n2 + 10 n23n3)*(-n23)
P2 = (-n023+ 50 n∞23 + 6 n123 - 8 n3+ 10 n2)*(-n23)
P2 = n023n23- 50 n∞23n23 - 6 n123n23 + 8 n3n23- 10 n2n23
P2 = -n0 + 50 n∞+ 6 n1- 8 n2- 10 n3
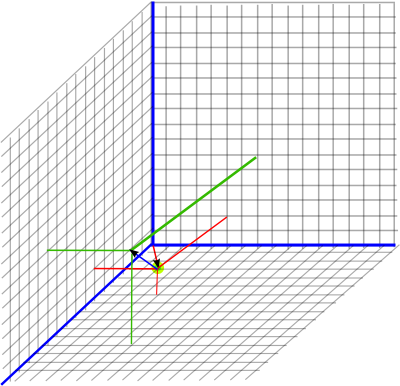
Combined Displacement and Rotation (displace then rotation)
Example
Starting from the previous position: (-n0+ 50 n∞ + 6 n1 + 8 n2 + 10 n3)
and both displace by (x=4, y=2, z=6) and applying a rotation of 180° around the x axis represented by: (n23)
Therefore:
m = (n23) (1 + 4 n∞1 + 2 n∞2+ 6 n∞3)
m = 1 n23 + 4 n23n∞1 + 2 n23n∞2+ 6 n23n∞3
m = 1 n23 + 4 ∞123 - 2 n∞3+ 6 n∞2
So applying the transform gives:
P2 = (n23 + 4 ∞123 - 2 n∞3+ 6 n∞2)*(-n0+ 50 n∞ + 3 n1 + 4 n2 + 5 n3)*(n23 + 4 ∞123 - 2 n∞3+ 6 n∞2)
P2 = (-n0+ 206 n∞ + 7 n1 -6 n2 -11 n3)