The position of a point in a plane can be represented by:
- Cartesian coordinates - Using two distance values on mutually perpendicular axis: P(x,y)
- Polar coordinates - Using a distance value and an angle: P(r,a)
Similarly a position in 3D space can be represented by:
- Cartesian coordinates - Using three distance values on mutually perpendicular axis: P(x,y,z)
- Spherical Polar coordinates - Using a distance value and two angles: P(r,a1,a2)
- Cylindrical Polar coordinates - Using two distance values and an angles: P(r,h,a)
For the special case of measuring the position on the surface of the earth see Geodetic (or Geographic) spatial reference frames.
Spherical polar coordinates could be thought of as being thought of as the angles being latitude and longitude and the distance being the distance from the centre of the earth. In this way any point in space can be represented (relative to the motion of the earth).
There may be other combinations for specifying a point in 3d using distances and angles. I think that any coordinate system would require at least one distance (cartographers can map a landscape using angles, but they need at least one distance to start with).
Conversion between Cartesian and Polar coordinates
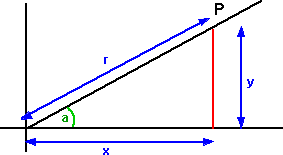
Polar to Cartesian coordinates
In two dimensions:
- x = r cos(a)
- y = r sin(a)
In three dimensions:
- x = r sin(a1) cos(a2)
- y = r sin(a1) sin(a2)
- z = r cos(a1)
Cartesian to Polar coordinates
In two dimensions:
- r = sqrt(x*x + y*y)
- a = atan(y / x)
Note: it is better to use the atan2(y,x) as explained here.
In three dimensions:
- r = sqrt(x*x + y*y + z*z)
- a2 = atan(y / x)
- a1 = asin(sqrt(x*x + y*y) / r) = acos(z / r)
Polar curves
In cartesian coordinates the equation of a curve tends to be given in the following form: y=f(x).
In the polar coordinate system it is often useful to give the equation of a curve in this form r=f(a), in other words it gives the distance from the centre in terms of the angle.
Some typical curves are given below,
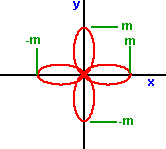
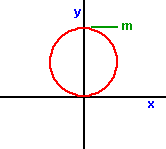
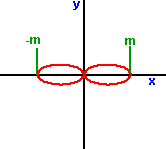
r = m sin(a)
r = m sin2(a)
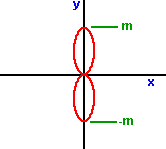
where sin2 is sin squared
r = m cos(a)
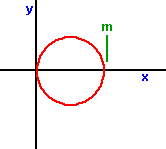
r = m cos2(a)
r = m sin (2a)
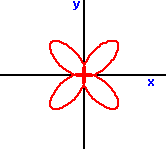
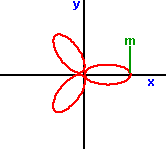
r = m sin (3a)
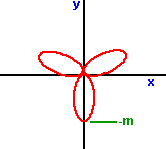
r = m cos (2a)