For a more theoretical approach see this page.
List Monad
| We can introduce a functor which takes any type and turns it into a list of that type. | 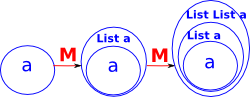 |
| We can draw this as an endo-functor. | 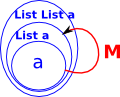 |
List - Natural Transformations
| The unit transform creates a single valued list | 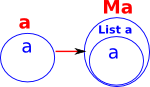 |
| The natural way to create a mult transform is a transform which flatterns a list of lists into a flat list. | 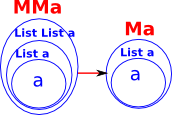 |
Lists Form a Free Monoid
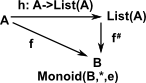 |
Lists form a free monoid, that is, this diagram commutes. |
This concept can be extended to other free structures see [R.M. Burstall and P.J. Landin, "Programs and their proofs, an algebraic approach", Machine Intelligence 4(1969)]
Lists as monads
map :: (x -> y) -> (M x -> M y)
This map applies function (x -> y) to every element of M
properties:
- map ID = ID since map :: (x -> x) -> (M x -> M x)
- map (g • f) = map g • map f
where:
- ID = (x -> x) and (M x -> M x)
- • = composite function
map is an example of a functor:
map :: (x -> y) -> (M x -> M y)
map :: f -> M f
That is, we can use M to represent the result of mapping elements and the result of mapping a function of elements. So M is a functor, a higher order function.
As usual we will call the two natural transformations 'unit' and 'join' and so adding these to the map gives:
| [] notation | M notation | ||
| • | map :: (x -> y) -> [x] -> [y] | map :: (x -> y) -> (M x -> M y) | |
| • | unit :: x -> [x] | unit :: x -> M x | |
| • | join :: [[ x ]]-> [x] | join :: M ( M x) -> M x |
List Monads in Haskell
The class (defines type) of any monad is:
class Monad m where return :: a -> m a (>>=) :: m a -> (a -> m b) -> m b |
The definition depends on what type, in this case the list monad can be defined like this:
instance Monad List where return x = [x] xs >>= f = concatMap f xs |
Comprehensions
[ t | q ]
where:
- t = term
- q = qualifier
defined by rules:
- [ t | x <- u] = map(λ x -> t) u
- [ t | /\ ] = unit t
- [ t | (p,q) ] = join [[ t | q] | p]
where:
- /\ = empty qualifier (usually [ t | /\ ] is just shown as [ t ])
- x -> u = generator
- u = list valued item
- (p,q) composition of terms
- (λ x -> t) = \ x.t = haskell form of λ operator
Equivalence between comprehensions and monads
| Monad | Comprehension | |
|---|---|---|
| map :: (x -> y) -> (M x -> M y) | [ t | x <- u] = map(λ x -> t) u | |
| unit :: x -> M x | [ t | /\ ] = unit t | |
| join :: M ( M x) -> M x | [ t | (p,q) ] = join [[ t | q] | p] |
Sets as monads
We can generalise to set notation
| Monad | Comprehension | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
||||||||||||||||||
| unitset :: x = { x } | unitset :: x = [ x ] | ||||||||||||||||||
|
|
where:
| • | U | = union | ||
| • | x | element of set | ||
| • |
|
= set of x | ||
| • |
|
= set of set of x |
comprehension notation:
| [ (x,y) | x <- | x | , y <- | y | ]set |