Here are some concepts which are used in functional programming (see: Meijer, Erik; Fokkinga, Maarten; Paterson, Ross. "Functional Programming with Bananas, Lenses, Envelopes, and Barbed Wire") and these concepts are also used in category theory.
| Notation | Functional Programming Term | Category Theory Term | Meaning (from here) |
|---|---|---|---|
| banana | catamorphism | tears down a structure level by level | |
| [( )] | lense | anamorphism | builds up a structure level by level |
| envelope | hylomorpism | builds up and tears down a virtual structure | |
| barbed wire | paramorphism | tears down a structure with primitive recursion |
Catamorphism and Anamorphism
| If we start with an algebra that has a binary operation (S,S)->S and, instead of supplying interal values we supply a symbolic value to represent a variable or unknown, we might build up a free algebra. |  |

- Catamorphism - initial algebra -> other algebra.
- Anamorphism
Catamorphism (banana)
Reduces the data structure to a required value.
Functional Programming Examples:
- Generalise the concept of fold.
Category:
Tree is a initial object in the category of F-algebras
Anamorphism (Lenses)
Upwards morphism - Builds an invocation tree as an explicit data structure.
Functional Programming Examples:
- Generalise the concept of unfold
- zip and iterate are examples of anamorphisms
A notation for ana(f) found in the literature is [(f)]. The brackets used are known as lens brackets.
In programming 'lenses' can be used as the functional equivalent of a 'reference' and they allow a functional (non-mutable) data structure to be used like an imperative (mutable) data structure. They do this by duplicating the data rather than using references to the same stucture. This allows functional programs to act on imperitive structures like databases in a purely functional way. Unlike other ways of doing this lenses are composable, that is, we can nest these structures to any debth (subject to memory constraints because of this duplication).
Laws
| get-put | P(S,G (S))=S |
| put-get | G(P(S,V))=V |
Where:
- P( , ) = put
- G( ) = get
Haskell Example
case class Lense[A,B] {
g: A => B
s: (B,A) => A
| {
DEF get (a:A):B=g(a)
DEF set(b:B,a:A): A=s(b,a)
References
Hylomorphism
Composition of an anamorphism and a catamorphism. Invocation tree is isomorphic to a function which processes lists.
Example Monoid
free monoid = list
- Fold is a catamorphism
- Unfold is a anamorphism
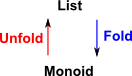
| Fold Left | 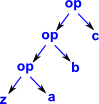 |
| Fold Right | 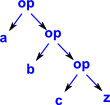 |
So the fold operation takes a list and a monoid and returns a value
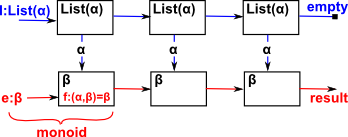
Googles MapReduce software framework.
Example Field
free field = tree?
