Maths - Category Theory - State Monad

In pure functional programs we can't have functions that depend on something other than the parameters of the function, or any 'side effects', that means that we can't have variables, input or output. If we followed this rigidly then functional programs would not be very useful. However, the monad gives us a workaround for this, a way to encapsulate these side effects so that most of the program is pure functional code.

As a simple example imagine we want to model the situation where we have a variable 'x' and we want to do operations to it like 'add 3 to it' or 'double it'. In a pure functional program we cant represent 'x' as a state variable or a variable in an object so all we can do is pass the 'variable' x as input and output to each function like this:

doubleIt x = x*2

add3ToIt x = x+3

So, if we want to add 3 and then double it, we would have to combine these functions like this:

doubleIt (add3ToIt x)

If there were a long sequence of operations to apply to the variable then this could get very messy (and there is the added complication that the order of the functions has to be written in reverse order).

The monad gives us a way to turn these nested functions into somthing that looks more like procedural code:

3 >>= add3ToIt >>= doubleIt >>= return

the functions '>>=' and 'return' are already defined in the Haskell preluse for the built-in monad class so, for now, we will use '>>==' and 'rtn' so that we can modify and experiment with them.

module Main where
  doubleIt x = x*2
  add3ToIt x = x+3
  rtn x = x
  x >>== f = f x

Prelude> :load monad0.hs
[1 of 1] Compiling Main          ( monad0.hs, interpreted )
Ok, modules loaded: Main.
*Main> 3 >>== add3ToIt >>== doubleIt >>== rtn
12
*Main>

In order to make the state a bit more general we could put the number in a wrapper like this:

data NumberWrapper n = NumberWrapper n deriving (Show)

So we modify our file as follows:

module Main where
  data NumberWrapper n = NumberWrapper n deriving (Show) 
  doubleIt (NumberWrapper x) = NumberWrapper (x*2)
  add3ToIt (NumberWrapper x) = NumberWrapper (x+3)
  rtn x = x
  x >>== f = f x

When run this gives the expected result:

Prelude> :load monad1.hs
[1 of 1] Compiling Main             ( monad1.hs, interpreted )
Ok, modules loaded: Main.
*Main> (NumberWrapper 3) >>== add3ToIt >>== doubleIt >>== rtn
NumberWrapper 12
*Main>

There is a built in class called Monad so we will monify our code to use that:

module Main where
  instance Monad NumberWrapper where
    return x = NumberWrapper x
    (NumberWrapper x) >>= f = f x

  data NumberWrapper n = NumberWrapper n deriving (Show) 
  doubleIt x = NumberWrapper (x*2)
  add3ToIt x = NumberWrapper (x+3)

When can load and run this as follows:

Prelude> :load monad2
[1 of 1] Compiling Main             ( monad2.hs, interpreted )
Ok, modules loaded: Main.
*Main> NumberWrapper 3 >>= add3ToIt >>= doubleIt >>= return 
NumberWrapper 12
*Main> 

Giving the same result, the built in Monad is defined as follows:

*Main> :info Monad 
class Monad m where 
  (>>=) :: m a -> (a -> m b) -> m b 
  (>>) :: m a -> m b -> m b  
  return :: a -> m a  
  fail :: String -> m a     
        -- Defined in GHC.Base  
instance Monad NumberWrapper -- Defined at monad2.hs:2:11-29
instance Monad Maybe -- Defined in Data.Maybe 
instance Monad IO -- Defined in GHC.IOBase 
instance Monad [] -- Defined in GHC.Base 
*Main>

State Monad

We can introduce a functor which takes any type and adds a state value.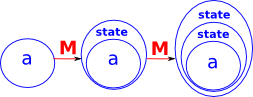
We can draw this as an endo-functor.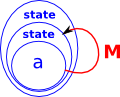

State - Natural Transformations

The unit transform adds the state value to type 'a'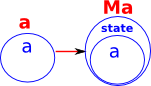
The mult transform combines the inner and outer state into a single state.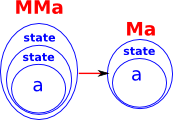

EuclideanSpace

home

Functional Programming and Category Theory