A 'presheaf' category is a special case of a functor category (see page here). It is a contravarient functor from a category 'C' to Set.
Since it is contravarient it is usually written:
Cop->Set
or
SetCop
So we have a functor from a category to the category of sets. This sends objects to sets and arrows to functions in a way that plays well with the objects. In category theory we don't tend to look inside objects but in set theory we look inside sets. S how can we define these morphisms? In order to work with sets it needs to preserve something to do with subsets.
Presheaf Category
In a presheaf category the object is a functor. |
|
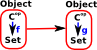 |
Morphisms are structure preserving maps between these functors. |
In the theory of topological space a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space.
Presheaf Examples
- A simplicial set is a presheaf on the simplex category
- A globular set is a presheaf on the globe category.
- A cubical set is a presheaf on the cube category.
Examples - Graph and Simplical ComplexesSee page here. |
 |
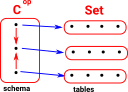
Example - Relational DatabaseSee page here. |
 |
Further Information
For a more general introduction to sheaves see the page here.