For more information about quaternions see this page. For infomation about how this page was derived see here.
Algebra Laws
Complex Numbers over the real numbers are a 'field' they have the following properties:
| addition | multipication | |
|---|---|---|
| unit element | 0 | 1 |
| commutative | yes | no |
| associative | yes | yes |
| distributive over addition | - | yes |
| inverse exists | yes | yes |
Multiplicative Group
If we ignore addition and treat complex numbers as a group then we have:
Cayley Table
| 1 | -1 | i | -i | j | -j | k | -k | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | -1 | i | -i | j | -j | k | -k |
| -1 | -1 | 1 | -i | i | -j | j | -k | k |
| i | i | -i | -1 | 1 | k | -k | -j | j |
| -i | -i | i | 1 | -1 | -k | k | j | -j |
| j | j | -j | -k | k | -1 | 1 | i | -i |
| -j | -j | j | k | -k | 1 | -1 | -i | i |
| k | k | -k | j | -j | -i | i | -1 | 1 |
| -k | -k | k | -j | j | i | -i | 1 | -1 |
- How this table was derived see this page.
- For more information about Cayley table in general see this page.
Cayley Graph
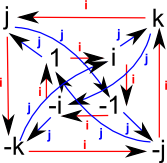
For more information about Cayley graph see this page.
Cyclic Notation
As can be seen on the Cayley graph above each generator has two 4-element cycles :
<(1 4 2 3)(5 8 6 7),(1 6 2 5)(3 7 4 8)
For more information about cyclic notation see this page.
Group Presentation
There are two generators.
<i,j | i² = j², j -1i j = i -1>
where: k=ij
For more information about group presentation see this page.
Group Representation
These are the root of -1 the identity matix. See this page for information about taking roots of a matrix. There are two such generators:
| [i] = |
|
[j] = |
|
k can be generated from i*j:
| [k] =[i][j]= |
|
For more information about group representation see this page.
