Prerequisites
If you are not familiar with this subject you may like to look at the following pages first:
Description
Dual numbers have the form:
a + w b
where:
w2 = 0
In the case where w2 = 0 we indicate this by replacing w with ε to give:
a + ε b
for dual vectors 'a' and 'b' can be vectors.
This is similar to the way that quaternions can be represented as a real part (scalar) and an imaginary part which is a vector.
For dual vectors either or both parts may be vectors.
Relationship to 3D Geometric/Clifford algebra
What is the relationship between dual vectors and 3D Geometric/Clifford algebra?
dual vectors has:
- two 3D vectors
3D Geometric/Clifford algebra has:
- two 3D vectors and two scalars
So could 3D Geometric algebra be a superset of dual vectors?
In 3D Geometric algebra squaring either of the vectors will give a scalar value, so if we dont have a scalar value then perhaps squaring them will give zero?
Applications of dual vectors
Dual vectors can be used to represent 'screw displacement' that is, a representation of velocity of a solid body, a combination of linear and angular velocity. (see kinimatics page on this subject).
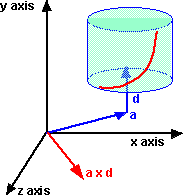
The components of a and d are known as plucker coordinates.
To represent this using the dual vector a + w b
then b = a x d
where:
- a is the distance from origin to axis vector.
- b is the w part of dual vector.
- d is the direction of the axis vector.
- x is the cross product

