Description
Double numbers have the same form as genralised complex number except that:
D² = 1
So in this case ω=D, the double operator.
In other words: double numbers are the same as complex numbers but with i²=-1 being replaced by D²=+1.
Another name for this is a 'split-complex' number. This is a two dimensional algebraic quantity, in other words elements in this algebra contain two scalar values. Both these dimensions square to +1 (so there is no square root of -1).
If we plot what happens to vertical(red) and horizontal(green) lines under the square transform we get the following plot:
| z plane | w plane | |
|---|---|---|
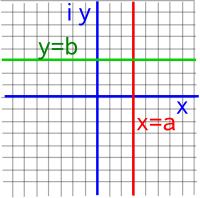 |
--> w=z² |
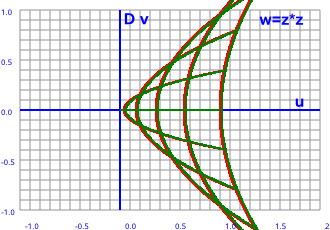 |
We can see that the results are all on the right hand (positive) side of the graph and that vertical and horizontal lines produce the same output.
These results are derived, along with other functions of double numbers, on this page.
As with most algebras, addition is defined by adding corresponding terms and the flavor of the algebra comes from the multiplication rules. If we denote the two dimensions by 1 and D then a '1' term is given by multiplying the same types together, a 'D' term is given by multiplying different terms. There are no sign changes. So we can define the algebra by the following table:
| a*b | b.1 | b.D |
| a.1 | 1 | D |
| a.D | D | 1 |
alternate basis:
idempotents
ee = e
e*e* = e*
at:
e = (1 - D)/2
e* = (1 - D)/2
Geometry
Represents Hyperbolic rotations. Hyperbolic trigonometry is explained on this page.
Algebraic Properties of Double Numbers
Division Exists
Yes, division exists exept where a=b or a=-b, for example:
(a1+D b1) / (a2+D b2)
has a solution provided that a2≠b2 and a2≠-b2 which would cause both components to be ∞.
Division is done by multiplying top and bottom by the conjugate as explained here.
commutative
Yes, in both addition and multipication, the order of its operands can be reversed without affecting the result:
x * y = y * x
We can easily check this by seeing that the multipication table is symmetrical about the leading diagonal.
associative
Yes, both addition and multipication is associative, the order of doing multiple operations is not important. For example:
x * (y * z) = (x * y) * z
For example:
(D * 1) * D = D * D = 1
D * (1 * D) = D * D = 1
distributive
* is distributive over + :
x * (y + z) = (x * y) + (x * z)
Modeling with Pauli Matrix
The number a + b D
can be represented by:
| a | b |
| b | a |
More information about Pauli matrices on this page.
Further Reading

