Maths - Multidimensional Algebra and Symmetry

Here we investigate how these algebras are related to geometry and especially the effect of changing the dimensions.

In Euclidean space (where both axes square to the same value) then we can rotate the basis vectors and the algebraic structure, as shown by the cayley tables, will remain the same. So there is a symmetry and the basis are arbitary provided that we are consistant about it.

In Minkowski space (where axis square to different values) there is only one rotation that gives the Cayley table structure that we have been working with (Orthonormal basis, standard diagonalised form).

Squaring Vectors

In the algebras that we are investigating, the Cayley table shows that squaring individual vector basis gives a scalar value, because all terms on the leading diagonal are scalar values. For example:

e1²=+1

or e3²=-1

Will any value in this algebra square to a scalar value? For instance if
e1²=+1 and e2²=+1 then what happens if we square a linear combination of:

(a e1 + b e2)²

where:

Squaring out the terms gives:

a²e1²+ a*b e1e2+ a*b e2e1 + b²e2

If the terms anticommute, that is: e1e2= -e2e1 then the middle terms will cancel out so we will get:

a²e1²+ b²e2

which will give a scalar value because the terms individually square to scalar values.

So, if terms anticommute then a linier sum of them will always square to a scalar value.

Distance Between Points

We want to investigate the effect of changing the basis but we need certain properties to remain the same, such a the distance between points on a solid object,

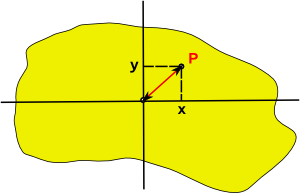
metric1

If the point P is given by:

xe1+ ye2

Then the square of the distance between P and the origin is given by:

x²e1²+ y²e2²

If we now choose different basis vectors the point P will now be given by:

x'e3+ y'e4

Then the square of the distance between P and the origin is given by:

x'²e3²+ y'²e4²

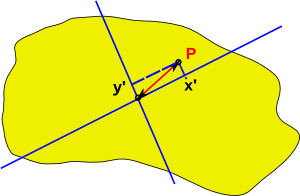
metric2

so for the distance to be the same in both cases:

x²e1²+ y²e2² = x'²e3²+ y'²e4²

Null Vectors, Idempotents and Nilpotents

Imagine that we have one dimension that squares to positive e1 (a space dimension) and another dimension that squares to negative e2 (a time dimension)

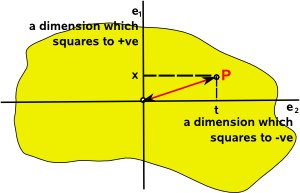
mink 1

In between the dimension that squares to positive and the dimension that squares to negative there must be dimensions that squares to zero:

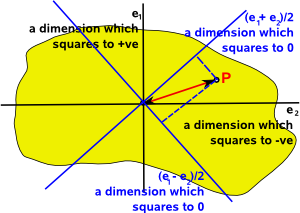
mink 2

So how do we rotate the basis vectors in this case? In Euclidean space (where both axes square to the same value) then we can rotate the basis vectors as follows:

e1'
e2'

=
cos(θ) -sin(θ)
sin(θ) cos(θ)
e1
e2

So what is the equivalent in Minkowski space (where axis square to different values)? is there a hyperbolic equivalent?:

n+
n-

=
cosh(θ) sinh(θ)
sinh(θ) -cosh(θ)
e1
e2

Anyway, it we set θ=45° we get:

or inverting to get ex in terms of nx we can add both sides of the above equations:

n+ + n- = (e1 + e2+ e1 - e2)/√2 = √2 e1

and subtracting the above equations gives:

n+ - n- = (e1 + e2- e1 + e2)/√2 = √2 e2

So ex in terms of nx is:

So if a section of the Cayley table for e1 and e2 is:

a*b
 b.e1 b.e2
a.e1 1 e1e2
a.e2 -e1e2 -1

(it is only a section of the Cayley table because I have not included row and column for scalar term although it is in table)

So e1 squares to +ve and e2 squares to -ve and e1 anticommutes with e2. When we change the basis to n+ and n- the products are:

n+n+=(e1 + e2)(e1 + e2)/2 = (e1e1 + e1e2 - e2e1 + e2e2)/2 = 0

n+n-=(e1 + e2)(e1 - e2)/2 = (e1e1 - e1e2 - e1e2- e2e2)/2
= (1 - e1e2 - e1e2+ 1 )/2 = (2 - 2e1e2)/2 = 1 - e1e2
= 1 - (n+ + n-)(n+ - n-)/2 = 1 - (n+n+ - n+n- + n-n+ - n-n-)/2
= 1 + (n+n- - n-n+)/2

n-n+=(e1 - e2)(e1 + e2)/2 = (e1e1 + e1e2 + e1e2- e2e2)/2
= (1 + e1e2 + e1e2+ 1 )/2 = (2 + 2e1e2)/2 = 1 + e1e2
= 1 + (n+ + n-)(n+ - n-)/2 = 1 + (n+n+ - n+n- + n-n+ - n-n-)/2
= 1 + ( n-n+ - n+n-)/2

n-n- = (e1 - e2)(e1 - e2)/2 = (e1e1 - e1e2 + e1e2+ e2e2)/2 = 0

putting these into a Cayley table gives:

a*b
 b.n+ b.n-
a.n+ 0 1 + (n+n- - n-n+)/2
a.n- 1 + (n-n+ - n+n-)/2 0

Note that this Cayley table has a completely different structure to the tables that we have worked with upto now in that:

So I'm not yet sure how to work with this?

To Do s

There are a lot of question marks and potential errors on this page.

When this is done it would be nice to link to Special Relativity topics:

It would also be good to attempt to relate to other Cayley tables with zero entries such as those derived from dual numbers.


metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

cover Mathematics for 3D game Programming - Includes introduction to Vectors, Matrices, Transforms and Trigonometry. (But no euler angles or quaternions). Also includes ray tracing and some linear & rotational physics also collision detection (but not collision response).

Other Math Books

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.