Representing the Characteristics of an algebra
On this page we describe properties that an algebra may have such as:
- commutative
- associative
- distributive
- inverse exists
Commutative
An operation is commutative if the order of its operands can be reversed without affecting the result. This is usually expressed in terms of arbitrary elements of the algebra (here denoted x and y).
| ( |
x * y = y * x |
This says that for all values of x and y then x * y is always equal to y * x. Below we will see that there are ways to express this without having to use arbitary variables.
Addition is commutative but multiplication may, or may not be, commutative. See table below. For example matricies and quaternions don't have commutative multiplication.
Associative
An operation is associative if the order of doing multiple operations is not important. For example:
| ( |
x * (y * z) = (x * y) * z |
Distributive
When there are two operations in this algebra say, + and *, then * is said to be distributive over + if:
| ( |
x * (y + z) = (x * y) + (x * z) |
Other Ways To Represent These Properties
So far we have described these algebraic axioms in terms of arbitrary variables named x,y and z. This is the easiest way to intuitivly understand the axioms, however when working with computers it may be better if we can find an altenative notation which eleminates these arbitrary variables, also this may help us to generalise to any structure which has a given system of axioms (see algebraic variety), that is we want to seperate the structure from the objects the structure works on.
To do this we need to abstract (lift) up a level and describe these properties in terms of its external properties. There are two mathematical subject areas on this site which take this approach:
- Category Theory - see functors and here.
- Combinatory Logic
Commutative Law
For instance in combinatory logic the commutative law, which we defined above:
| ( |
x + y = y + x |
We change + as a prefix rather than an infix operator:
| ( |
+(x,y) = +(y,x) | |
| +(x,y) = (C+)(x,y) |
Where C means: swap functions as explained on the combinatory logic page.
So we can cancel out the elements (x,y) and just represent the commutative axiom as:
+ = C(+)
So using operators we don't have to describe axioms in terms of arbitrary elements.
Associative Law
We can also 'lift' the associative law, on the category theory pages the associative law, which we defined above:
| ( |
x * (y * z) = (x * y) * z |
On this page we changed * which acts as an infix operator to μ which acts as a prefix function and so we get:
| μ(x,μ(y,z)) = μ(μ(x,y),z) | prefix version of above |
| μ(id×μ)(x,y,z) = μ(μ×id)(x,y,z) | rearrage to make function of (x,y,z) |
| μ•(id×μ) = μ•(μ×id) | 'lift' that is cancel out (x,y,z) |
Table of Axioms for some Algebras
| * distributive over + | Multiplication commutative | Multiplication associative | |
| Real Numbers | yes | yes | yes |
| Complex Numbers | yes | yes | yes |
| Quaternions | yes | no | yes |
| Octonions | yes | no | no |
| Vectors | yes | no | no |
| Matricies | yes | no | yes |
| Multi Vectors | yes | no | no |
Modelling these properties using computers
How do we apply and work with these properties using computers? Can we automatically apply these rules to solve equations?
As an example we will look at determining these laws in group theory.
Can we determine these properties from the Cayley Table? Well the distributive property does not apply to a single operation so we will investigate the other properties.
Commutative
It is easy to relate the commutative properties of the operation to the Cayley table. Reversing the order of the operands is the same as swapping columns and rows, so an operation is commutative if it is symmetrical about the leading diagonal. Some operations are anti-commutative and we can quickly see this also if reflecting in the leading diagonal changes the sign.
Associative
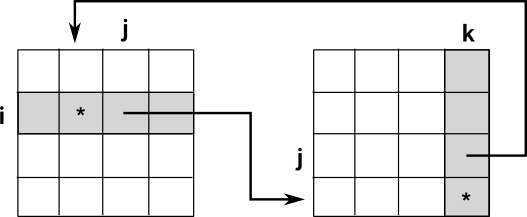
Inverse exists

