note: The concept of a 'field' in algebra is different from the concept of a 'vector or scalar field' which occurs in geometry and physics. (although there is a connection with vectors as we shall see).
Definitions
A field is a commutative ring with unity.
An integral domain is a commutative ring with unity and no zero-divisors.
A zero-divisor is a non-zero element 'a' of a commutative ring 'R' such that there is a non-zero element b![]() R with ab=0
R with ab=0
Axioms
| axiom | addition | multiplication | both |
|---|---|---|---|
| associativity | (a+b)+c=a+(b+c) | (a*b)*c=a*(b*c) | |
| commutativity | a+b=b+a | a*b=b*a | |
| distributivity | a*(b+c)=a*b+a*c (a+b)*c=a*c+b*c |
||
| identity | a+0 = a 0+a = a |
a*1 = a 1*a = a |
|
| inverses | a+(-a) = 0 (-a)+a = 0 |
a*a-1 = 1 a-1*a = 1 if a≠0 |
Examples of Fields
Examples include:
- the real number field
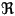 .
. - the complex numbers C.
- the rational numbers Q.
- finite fields.
- various fields of functions.
Some algebras that are not fields are vectors (unless a commutative multiplication is used), matrices (not commutative) and quaternions (not commutative).
Properties
Every field is an integral domain
Extension Field
A Field 'E' is an extension field of a field 'F' if F is a subset of E and the operations of F are those of E restricted to F.
Polynomial Domain
Every algebraic number field can be obtained as the quotient of the polynomial domain Q[x] by the principle ideal generated by an irreducible polynomial.
Theorems
The degree of an extension Q(r) always matches the degree of the irreducible polynomial to which r is a root.
The degree of a normal extension matches the degree of its Galois group.
| p(x) | F Field |
E Extension |
splitting of p(x) |
|---|---|---|---|
| x²-2 | Q | Q(√2) | (x-√2)(x+√2) |
| Q[z]/<z²-2> | (x-z)(x+z) | ||
| x³-2 | Q | Q(w,³√2) | (x-³√2)(x-w ³√2)(x-w² ³√2) |
| Q(w)[z]/<z³-2> | (x-z)(x-w z)(x-w² z) | ||
| Q(³√2)[y]/<y² + y + 1> | (x-³√2)(x-y ³√2)(x-y² ³√2) | ||