On this page we first define the Kronecker product in terms of matricies, we then try to interpret this in more general terms.
We multiply each term in matrix [A] by the whole of matrix [B] as follows:
| [A] |
|
This can be combined into a single matrix as follows:
| [A] |
|
We can represent this in tensor notation:
(Pij) km = δijδkm
Possible Interpretation
The Kronecker product C=A![]() B can be thought of as creating an algebra C from two smaller algebras A and B.
B can be thought of as creating an algebra C from two smaller algebras A and B.
If A and B represent linear operators on different vector spaces then A![]() B represents the combination of these linear operators. The important point is that they are acting in different vector spaces, when we combine linear operators within the same vector space be use conventional multipication operations as described elesewhere on this site.
B represents the combination of these linear operators. The important point is that they are acting in different vector spaces, when we combine linear operators within the same vector space be use conventional multipication operations as described elesewhere on this site.
Example
In order to illustrate now to calculate the Kronecker product here is an example:
| If A = |
|
|||||||||
| and B = |
|
calculate A![]() B
B
is worked out as follows:
| [A] |
|
multiplying out the terms gives:
| [A] |
|
Properties
[I]![]() [I] = [I]
[I] = [I]
([A1]+[A2])![]() [B] = [A1]
[B] = [A1]![]() [B]+[A2]
[B]+[A2]![]() [B]
[B]
[A]![]() ([B1]+[B2]) = [A]
([B1]+[B2]) = [A]![]() [B1]+[A]
[B1]+[A]![]() [B2]
[B2]
([A]![]() [B1])-1= [A]-1
[B1])-1= [A]-1![]() [B]-1
[B]-1
Cartesian and Tensor Products in other Algebras
| Graphs | Matrix | |
|---|---|---|
| Cartesian | Cartesian product | Kronecker sum |
| Tensor | tensor product | Kronecker product |
Cartesian and tensor products not only occur in matrix algebra but also occur in other algebras. It may help intuative understanding to look at these products in graph theory on the page here.
Cayley Table and Checkerboard Pattern
Let the components of the matrix be operators, in this case:
- 1=reals
- x = non-real type
We can then represent the multipication of these types in a psudo-matrix.
| One of the simplest operator matrix is: A= |
|
We can use a Kronecker product to combine this with a similar operator matrix:
| B = |
|
So useing a Kronecker product gives:
| [A] |
|
= |
|
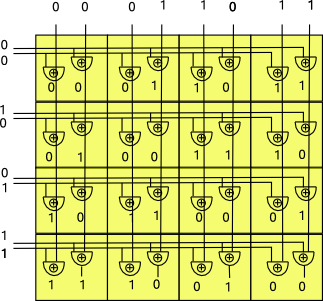
There is an easy way to calculate this result for any dimension, provided that the terms are encoded in bit order, that is the low order bit is one of the term contains an 'x', the next bit is a one if the term contains a 'y', and so on.
So the two individual tables are:
| If A = |
|
||||
| and B = |
|
The Kronecker product is then given by the exclusive or of each of the bits taken separately:
| [A] |
|
The exclusive or function (sometimes confusingly given the symbol: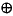 ) is 1 when either of the inputs is 1, but 0 if both of the inputs are 1.
) is 1 when either of the inputs is 1, but 0 if both of the inputs are 1.
A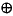 B B |
0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
So if we apply this to each of the terms in the table we get:
Example
What is the product of e4 and e5?
Since the operators are in bit order then:
e4 = 100 and
e5 = 101
taking the exclusive or of each bit in turn we get:
001
which is e1

