A one sided surface which cannot be embedded in 3D space without intersecting itself. There are no external boundaries, every edge connects two faces. (A punctured projective plane is equivalent to a Möbius band)
The simplest representation of a projective space would be like this: There is only one vertex, although it is drawn twice. There are two directed edges: 'a' and 'b' which go from 'x' to 'x'. |
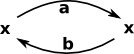 |
If we apply 'a' we go from 'x' to 'x' but we are not in the state we started in, we can then apply 'b' to get back to where we started. This diagram does not seem to fully capture this behavior so we will elaborate it. First we will represent it as a triangulation.
Here we insert a second vertex 'y' part of the way along the previous arrows. This may look similar to triangulations of other surfaces such as the torus, but note that now the direction of the edges is now clockwise around the outside. |
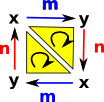 |
We still have each vertex appearing on the diagram twice. In order to represent this in ordinary space we need to merge the duplicates. To do this we will embed the rectangle in 3D space. We can then lift up the edges called 'x' and bring them together. At the same time we can lower the points 'y' and bring them together.
|
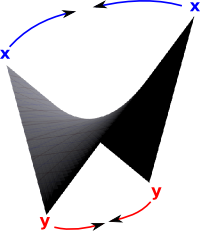 |
This attempts to produce a space with negative curvature everywhere (like a saddle - going up in the x dimension and down in the y dimension). Its not possible for a finite shape to have that property everywhere so I conclude that its not possible to do this in 3D space.
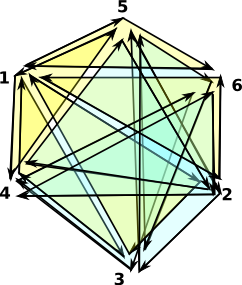
A Minimal Triangulation of the Surface of a Projective Plane
Projective Plane - No boundaries, every edge is connected to two faces: (3) -> projectivePlane()
+1 2 3+
|1 3 4|
|1 2 6|
|1 5 6|
(3) |1 4 5|
|2 3 5|
|2 4 5|
|2 4 6|
|3 4 6|
+3 5 6+
Type: FiniteSimplicialComplex(VertexSetAbstract) |
Above is my attempt to draw, with each vertex appearing once, this makes the diagram very cluttered and hard to understand. Its easier to draw if nodes 4,5 and 6 appear twice as below:
Note: edges 4->5, 5->6 and 6->4 connect two faces but they wind in the same direction. |
|