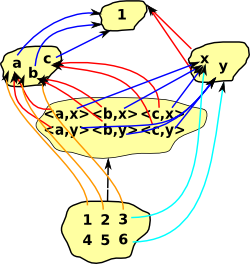
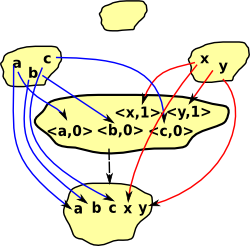
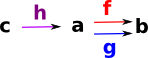Here we look at properties of categories that are common across all concrete categories from different branches of mathematics. As discussed earlier we are trying to find the properties of a category from its external interactions and universal properties give us a way to do this. In particular we may be looking for unique arrows (morphisms) that have some particular property.
In universal properties there is a unique isomorphism somewhere, this gives the 'best' of such a property.
Universal constructions happen in dual pairs:
Limits and Colimits
A limit is a way to take a diagram and encapsulate its properties into one object as simply as possible.
This is a generalisation that includes:
|
 |
Linked to the ideas of universal properties and adjoint functions
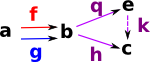
These generate a construction (c) which depends on the diagram such that:
- All triangles commute.
- Any other object c' can be factored through c without loosing information (there is a unique arrow to make the cones commute).
The first condition makes 'c' general enough to capture the essence of the construction.
The second condition makes sure that it is only just general enough (no junk).
For more information about limits and colimits see this page.
Cone and Cocone
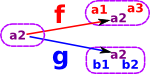
This is also called a wedge. For a given pair there may be many wedges. We look for a 'best possible' wedge .
example: highest common factor.
A cone/cocone can be added on to an existing diagram.

| Cone | Cocone | |
|---|---|---|
| A cone/cocone is defined by the tuple: (X,f,g). | 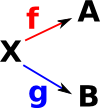 |
 |
| We can give this a universal property if, for other tuples (Xi,fi,gi), there is an arrow m known as the mediating arrow. This makes (X,f,g), in some way, the 'best' for that construction. | 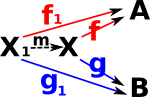 |
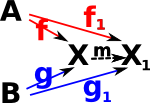 |
| Example in set | union
|
intersection
|
Initial and Terminal Objects
These are related to the identity elements of an algebra.
In some cases (group, vectors) an object is both initial and terminal, in this case it is called a zero object or null object.
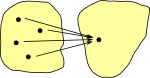
Terminal objects give a category theory version of the concept of 'element' in set theory. 1 -> A allows us to pick out an arbitrary element of the set.
Terminal (more on page here) |
Initial (more on page here) |
|
|---|---|---|
 |
 |
|
| Notation | 1 | 0 |
| generalisation | a kind of limit | a kind of colimit |
| universal cone over diagram |
|
|
| examples: set: | {1}or {a} ... set with one element (singleton) |
Ø = {} empty set |
| group (null object) | trivial group (just identity element) | trivial group (just identity element) |
| topological space | single point | empty space |
| poset | greatest element (if exists) | least element (if exists) |
| monoid | trivial monoid (consisting of only the identity element) | trivial monoid |
| semigroup | singleton semigroup | empty semigroup |
| Rng | trivial ring consisting only of a single element 0=1 | ring of integers Z |
| fields | does not have terminal object | does not have initial object |
| Vec | zero object | zero object |
| Top | one-point space | empty space |
| Grf | graph with a single vertex and a single loop | the null graph (without vertices and edges) |
| Ω-Alg algebra with signature Ω |
initial (term) algebra whose carrier consists of all finite trees. | |
| Cat | category 1 (with a single object and morphism) | empty category |
Equaliser and Coequaliser
For more information about equalisers and coequalisers see this page.
| Equaliser | Coequaliser | |
|---|---|---|
| universal cone over diagram |
|
|
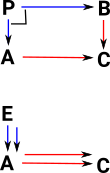
An equaliser is an arrow 'h' which makes 'f' and 'g' equal. |
A Coequaliser is an arrow 'h' which makes 'f' and 'g' equal. Universal Property: 'k' is a unique arrow known as the mediator. |
|
| this is equivalent to the following diagrams commuting |
that is: |
|
| equaliser is monic | coequaliser is epic | |
| Related concepts in set theory. |
Subset - every subset of a set occurs as an equaliser. See also subobject classifier in topos theory.
|
Equivalence - a binary relation which is:
|
Relationship of Equaliser to Pullback
If the category A is split into two categories A&B then the equaliser becomes a pullback. See pullback on this page. |
 |
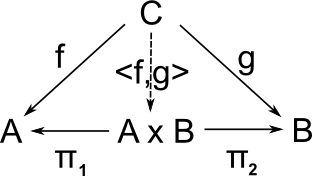
Product and Sum
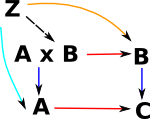
Product |
Sum |
|
|---|---|---|
| universal cone over diagram |
|
|
 |
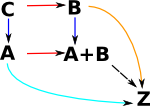 |
|
| generalisation | a kind of limit | a kind of colimit |
| set example | cartesian product
{a,b,c}*{x,y}= |
disjoint union
{a,b,c}+{x,y}= |
| group | the product is given by the cartesian product with multiplication defined component wise. | free product the free product for groups is generated by the set of all letters from a similar "almost disjoint" union where no two elements from different sets are allowed to commute. |
| Grp (abelian) | direct sum | direct sum the group generated by the "almost" disjoint union (disjoint union of all nonzero elements, together with a common zero) |
| vector space | direct sum | direct sum |
| poset | greatest lower bound meet |
least upper bound join |
| base topological space | wedge | |
| POS | greatest lower bounds (meets) |
least upper bounds (joins) |
| Rng | ||
| Top | the space whose underlying set is the cartesian product and which carries the product topology | disjoint unions with their disjoint union topologies |
| Grf | ||
| category | objects: (a,b) morphism: (a,b)->(a',b') |
|
tensor products are not categorial products.
In the category of pointed spaces, fundamental in homotopy theory, the coproduct is the wedge sum (which amounts to joining a collection of spaces with base points at a common base point).
Sum
When generating a sum for objects with structure then the structure associated with the link can be added to the sum object.
Product
Products for groups are discussed on this page.
Pullbacks and Pushout
Pullback:
- Generalisation of both intersection an inverse.
- If a category has binary products and equalisers, then it has pullbacks.
In programming terms it is related to the concept of indexing.
The pullback is like a type of division for function composition, in other words if multiplication is function composition then what is division? This comes in left and right flavors that is:
if h = g o f
- We know f and h, how do we find g?
- We know g and h, how do we find f?
More about pullbacks on page here.
Completeness and Cocompleteness
- a category is complete if every diagram from a small (i.e. finite) category to it has a limit
- a category is cocomplete if every such functor has a colimit.
| Competeness | Cocompeteness |
|
|---|---|---|
| set example |
|
|
| Set | ||
| Grp | ||
| Rng | ||
| Vec | ||
| Top | ||
| Grf | ||
| Cat |
Exponential
This is a universal structure but not a limit.
Example of a Limit
More about limits on this page.
Lets look at a Category of Subsets (could also be looked at as a poset, which forms a lattice, but the diagrams seem more instructive if we show it as subsets) where the objects are subsets and the arrows preserve these subsets:
So, as an example, we take these three subsets:
|
|
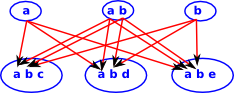 |
There are various other subsets which have arrows to our original diagram:
(on this diagram I have shown an internal representation of the arrows rather than just the arrows themselves) |
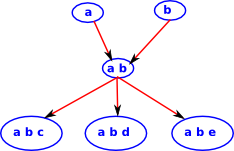 |
But only one of these has arrows from all the others. |
We can see that this limit represents the biggest subset which is common to our original diagram. In some ways limits like this represent a more sophisticated form of 'type', so all the objects in the first diagram are a 'type' which contain {a,b}.
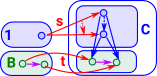
Universal Morphism as a Comma Category"The notion of a universal morphism to a particular colimit, or from a limit, can be expressed in terms of a comma category. Essentially, we create a category whose objects are cones, and where the limiting cone is a terminal object; then, each universal morphism for the limit is just the morphism to the terminal object. "- academickids.com See page here. |
 |