Universal algebra is an attempt to generalise algebra so that the nature and properties of algebras can be studied independently of any specific algebra. So we are not looking at the specifics of 'number algebra' or 'matrix algebra' for instance but we are looking at general properties that they may, or may not, have.
see model theory on page here.
Algebraic Theories and Models
An 'algebraic theory' is a set of 'n-ary' operation signatures (see syntax below for definition) together with a set of axioms (defined by a set of equations). This defines the algebra at a high level, such as the concept of a group, but not necessarily what type of group it is.
An 'algebraic model' is a set of 'n-ary' operations which are completely defined and can be used to do actual calculations. It is a model of a given theory if it obeys the axioms for that theory.
Syntax and Semantics
We can divide a algebra into syntax and semantics:
Syntax
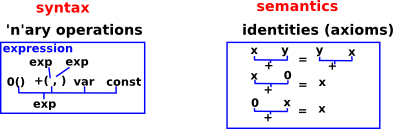
We can think of a algebra as being a set which is closed under some 'n-ary' operations. To explain this a bit further, think of the functions and operations in an algebra in a form like this:
f: Xn->X
So, for example, we may have an operation (say addition) that takes two operands and returns a single value. We might represent this like this:
X+X->X
This is known as 'infix' notation where the operation symbol is put between the values it is operating on. In order to generalise this to any number of operands, we will change to prefix notation, this also emphasises that it is a function like this:
+(X,X)->X
We can represent (X,X) as X². So when we generalise from 'binary' to 'n-ary' operations we get the form here:
f: Xn->X
We can have multiple operations so we use capital sigma to indicate this:
Σ f: Xn->X
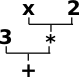 |
Using these function signatures we can build up expressions of any complexity. This is built up recursively, that is, an operand may be not only a constant of a variable but also another expression. The expression on the left would usually be written: 3+x*2 but I have drawn it at a tree structure to emphasise its recursive nature. |
So the syntax defines how expressions are built up, to define the result of calculation we need the semantics:
Semantics
To find the result of an operation we need to do the arithmetic or whatever the operation is. However there is a lot we can find out about about the result without actually doing the calculation. Algebras have a set of axioms and rules.
We often think of this as a sort of 'logic' layer over the algebra.
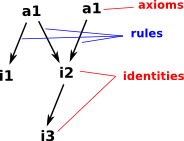 |
Valid equations for an algebra are called identities, or if they are taken as a starting point without proof, then they are called axioms. |
Universal Algebra
Here, rather than just looking at an algebra and its properties in isolation we look at all algebras and how they relate to each other.
There are two ways to define an algebra:
- We can start with the syntax, a model is a structure for interpreting a language. Often this is a set of n-ary operations with the requirement that each of these operations must be closed.
- We can start with a set of identities which represent an algebraic theory.
We could either start with a set of operations and then derive a set of identities or axioms that define that algebra or we could start with the identities and find operations that satisfy these identities (known as varieties).
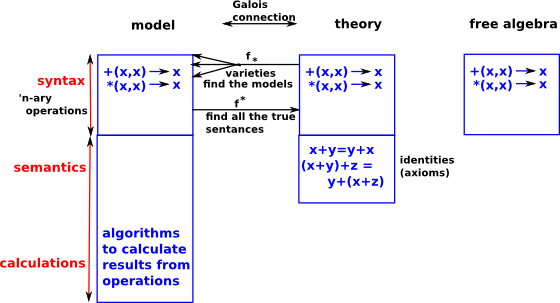
Galois connection is explained on the page here, in category theory terms it is an adjunction.
This Galois connection is between an algebra and pairs of terms (equations).
Theorems
- f*(f*(α)) is the theory with axioms α
- A syntax is axiomatizable if there is a theory θ such that m
 μ iff m is a model of θ.
μ iff m is a model of θ.
Natural Number Example
Free Algebras
If we have a signature(syntax) for an algebra but no identities, then this is known as a free algebra.
Combining Algebras
We can combine whole algebras in various ways to produce new algebras. This is like a set of operations operating at a higher level than the operations that make up the algebra itself.
| meta operation | |
|---|---|
| homomorphic images | a structure preseving map between the two algebras. This allows us to define various levels of 'equality' between the algebras. |
| subalgebras | In some cases we can 'factorise' an algebra into components. |
| product algebras |
|
Universal Algebra
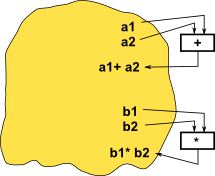 |
+(a1,a2) -> A An algebra has a number of binary (or n-ary) operations which map 2 elements to a single result |
Categorisation of Algebras
The type of an algebra is a sequence of the fundamental operations on that algebra:
| algebra | signature | type | identities |
|---|---|---|---|
| groupoid | (2) | (G; •) | |
| semigroup | (2) | (G; •) | associative: x•(y•z) = (x•y)•z |
| semilattice | (2) | (G; •) | associative: x•(y•z) = (x•y)•z commutative: x•y = y•x idempotence: x•x = x |
| monoid | (2,0) | (G; •,{1}) | associative: x•(y•z) = (x•y)•z identity: x•1 = x = 1•x |
| group | (2,1,0) | (G; •,-1,{1}) | associative: x•(y•z) = (x•y)•z identity: x•1 = x = 1•x inverse: x•x-1 = 1 = x-1•x |
| abelian group | (2,1,0) | (G; •,-1,{1}) | x•(y•z) = (x•y)•z x•1 = x = 1•x x•x-1 = 1 = x-1•x x•y = y•x |
| quasigroup | (2,2,2,1) | (Q; •,/,\,-1,{1}) | (x•y)/y=x ; y=x\(x•y) x•(x/y)=y ; x=(x/y)•y |
| loop | (2,2,2,1,0) | (Q; •,/,\,-1,{1}) | x•1 = x = 1•x x•x-1 = 1 = x-1•x |
| semiring | (2,2) | (R; +, •) | 2 associative, 2 distributive |
| ring | (2,2,1) | (R; +, •,-) | 2 associative, 2 distributive, 1 commutative |
| field | (2,2,1,0) | (K; +, •,-1,{0}) | |
| lattice | (2,2) | (L; /\,\/) | associative: x•(y•z) = (x•y)•z commutative: x•y = y•x idempotence: x•x = x |
| bounded lattice | (2,2,0,0) | (L; /\,\/,0,1) | associative: x•(y•z) = (x•y)•z |
| heyting | (2,2,2,0,0) | (L; /\,\/,->,0,1) | associative: x•(y•z) = (x•y)•z |
| boolean | (2,2,1,0,0) | (B; /\,\/,¬,0,1) | |
| power set | (2,2,1,0,0) | (P; |
The signature is a sequence of non-negative integers where each integer represents a function from An to A:
| element of signature | function | description |
|---|---|---|
| 0 | () -> A | a function with no input, this represents a significant element of A such as 0 or 1 |
| 1 | (A) -> A | unary operation such as inverse |
| 2 | (A,A) -> A | binary operation such as addition or multiplication |
| n | (An) -> A |
Universal Coalgebra
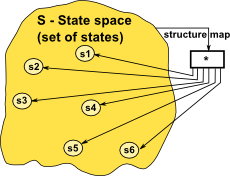 |
op(S) -> (s1,s2,s3...) A coalgebra consists of a state space (set of states) and a structure map An operation in a coalgebra maps a single input to multiple outputs. The map S -> F(S) maps the dynamics and so is a functor. |
On this page we looked at category theory, we can use these methods to relate algebras and coalgebras by reversing the arrows.
Coalgebras can represent state based computation, dynamic systems whose state changes over time, such as state based machines, petri nets, Turing machines etc.
Vectors and Modules
Vector operations have aspects of both algebras and coalgebras.
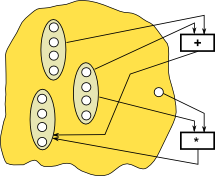
Duality between algebra and coalgebra
| algebra (or f-algebra) | coalgebra | |
|---|---|---|
| data types | state based systems | |
| deals with | construction finite data elements |
deconstruction potentially infinite data elements |
| proof principle | induction | coinduction |
| operation | An algebra has a number of binary (or n-ary) operations which map 2 elements to a single result | An operation in a coalgebra maps a single input to multiple outputs. |
| states | F(X) -> X | X -> F(X) |
| computing | functional programming | object oriented programming (an object is a finite state machine which we act on by sending it messages) |
| data type | detemined by its constructors | destructors point out of class |
Lattice
An important algebra is a lattice (see page here), it has two operations:
- meet /\
- join \/
identities:
| identitiy | meet | join |
|---|---|---|
| commutativity | x /\ y = y /\ x | x \/ y = y \/ x |
| associativity | (x /\ y) /\ z = x /\ (y /\ z) | (x \/ y) \/ z = x \/ (y \/ z) |
| idempotency | x /\ x = x | x \/ x = x |
| absoption laws | x \/ (x /\ y) = x | x /\ (x \/ y) = x |
there are also distributive laws which may, or may not, apply for a paricular lattice.
| identitiy | |
|---|---|
| distributive | x /\ (y \/ z) = (x /\ y) \/ z |
| distributive | x \/ (y /\ z) = (x \/ y) /\ z |
Lattices are of interest here, not just because ther are algebras but because they represent how algebras relate to each other.
Theorem - Every finite algebra is isomorphic to a direct product of directly indecomposible algebras. (not true of infinite algebras)
That is, we can build up algebras from (subdirect) products of certain 'building block' algebras.
Classes and Varieties of Algebras
A set of algebras is a 'class'. This class is related in some way, for instance:
| H(K) | class of all homomorphic images of K |
| S(K) | class of all subalgebras of K |
| P(K) | class of all product of K |
A variety is closed under H, S and P:
V(K) = HSP(K)
Birkhoffs HSP Theorem
A class K algebras of type τ is equationally definable if and only if it is a variety.
Birkhoff's HSP theorem identifies model classes of certain equational theories as being those classes (varieties) closed under morphisms (H), (iso to) subalgebras (S), and (iso to) products (P).
Relationship to Category Theory
There are two approches to working with algebras in category theory, ether,
- Based on monads
- Based on Lawvere theory
Lawvere Algebraic Theory
Bill Lawvere introduced a new categorical method for doing universal algebra. This defines an algebraic theory as:
- a category with finite products
- possessing a “generic algebra” (e.g., a generic group)
- then define a model of that theory (e.g., a group) as a product-preserving functor out of that category.
This is a category T with finite products.
Models of T are finite product preserving functors T->Set.
Algebraic theories (left exact theories) are categories T with finite limits, whose models are finitely continuous functors T->Set.
