Let A be a concrete category; that is, A is equipped with a forgetful functor:
U:A->Set
to the category of sets. For some authors, such a category is called ‘concrete’ only if U is representable, but that follows in all the cases below; in particular, if A has free objects (that is, if U has a left adjoint F), then U is representable by F(1), where 1 is a singleton.
Definition a concrete category A is algebraic if:
- A has free objects.
- The category A has all binary coequalizers.
- The forgetful functor U preserves and reflects extremal epimorphisms.
Definition a concrete category A is monadic if:
- A has free objects.
- The adjunction F
 U is monadic.
U is monadic.
Definition an algebraic (or monadic) category is bounded if:
- For some cardinal number κ and every κ-directed colimit in A, the universal cocone is jointly surjective in Set.
Definition - an algebraic (or monadic) category is finitary if:
- For every finitely directed colimit in A, the universal cocone is jointly surjective in Set.
Note that this a weakening of the condition that the forgetful functor U is fintary (that is, that U preserves directed colimits); every universal cocone in Set is jointly surjective, but not conversely.
Definitions
An algebraic theory is: a small category 'T' with finite products.
An algebra for the theory 'T' is a functor A: T -> Set preserving the finite products.
Alg T is the category of the algebras of T.
Example - Sets
| algebraic theory T1 for sets | 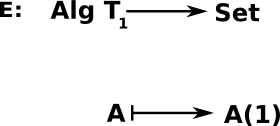 |
