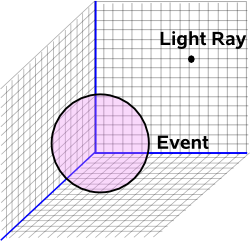
On this page we defined 'distance' as √(-Δt²+Δx²+Δy²+Δz²) which made the rectangular coordinate system (t,x,y,z) very strange. For instance, all points on the null cone are zero distance from the apex, however these points are not necessarily zero distance from each other.
| Minkowski Space M | Twister Space PN |
|---|---|
 |
|
One possible way to analyse such a space might be to map it to another space without such problems.
Possible spaces we might map to are:
- Projective Space
- Conformal Space
- Twister Space
On this page we will discuss twister space See Roger Penrose - The Road to Reality chapter 33 (book shop at bottom of page).
The mapping to twister space maps light rays to points, this can be expected since there is zero distance between the spacetime 'points' on the lightray.
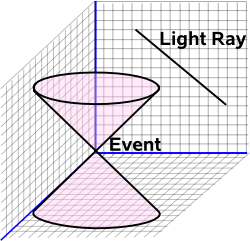
It then maps events from a point in Minkowski space to a sphere in twister space. We can then see how the rays on the light cone can be zero distance from themselves and from an event but non-zero distance from other light rays that intersect the event.
Or, to put it the other way round, events are made up of a set of points representing the light rays involved. So the null cone is a sphere consising of all possible light rays that could intersect with the event.