Here we will investigate the apparent curvature caused by space and time squaring to different signs.
In space we can identify a point by 3 scalar values: (x,y,z). Similarly in space-time we can identify a point (representing an event say) by 4 scalar values: (t,x,y,z). So is space-time just a matter of increasing our rectangular coordinate system from 3 dimensions to 4?
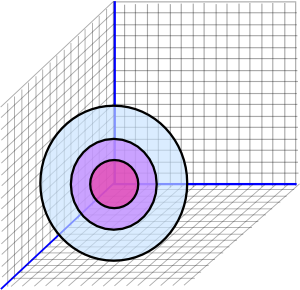
There is another difference, in space we would represent the distance between two points as:
distance = √(Δx²+Δy²+Δz²)
Which means that points of equal distance from the origin (we will use the origin to represent the observer as the origin has no special significance in euclidean space) can be represented as spheres:
However in space-time then we either use a metric where (-+++):
- space squares to positive
- time squares to negative
or (+---):
- space squares to negative
- time squares to positive
The second seems to be more common in physics literature but I don't think it makes much difference at this stage so I think I'll use the first alterative for now to make it easier to compare with the way that we usually measure things in space. So we will represent the distance between two points as:
distance = √(-Δt²+Δx²+Δy²+Δz²)
This change of sign caused by time squaring to negative causes a big difference when plotting points of equal distance from the origin which now become parabolas:
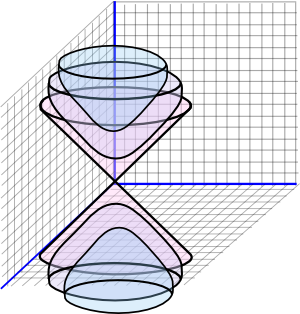
So in space-time we can still plot t,x,y,z on a rectangular coordinate system but we have to be careful about its meaning, we can't draw any conclusions from the proximity of points in space to their closeness by the measure that we have chosen.
The way we have chosen to measure the concept of 'distance' between points then goes on to affect most other concepts in geometry. For instance, the definition of a 'straight line' is usually the shortest distance between two points, so should we define a straight line in space-time in terms of minimising this distance function √(-Δt²+Δx²+Δy²+Δz²). Although changing the definition of distance could affect what is a straight line does it in this instance? After all we still experience light rays as traveling in straight lines in 3D space (until we go on to general relativity).
To reinforce the strangeness of defining distance in this way lets look at some of the consequences:
The outer cone shown above (the null cone: two cones meeting at the same point) shows all the points that are a zero distance from the origin (where Δt²=Δx²+Δy²+Δz²). However although they are all a zero distance from the origin they are not all zero distance from each other!
The distances to points outside the null cone are imaginary (Δt²>Δx²+Δy²+Δz² so distance=√-ve ) indicating that we would have to go faster than the speed of light to reach these points.
So not only is this not a Euclidean space or a vector space (a=b and b=c does not imply a=c) it is very hard to imagine there could be a transform that would map this onto a Euclidean space.
How can we analyse such a situation? I think we have to treat the origin as the position of the observer and accept that the space will appear different to different observers.
Conjugate Space and Invariance
In Euclidean space the distance from the origin to the end of the vector (a scalar value) is given by:
d = √(v•v)
where:
- v = vector
- d = distance (scalar)
Although we have used the dot product we could also have used the geometric product (since the cross product with itself is zero: v×v=0).
On this page we are working in Minkowski space so we need to modify the above expression to give our definition of distance.
So in addition to the space-time definition:
v = (t,x,y,z)
We also need to define its conjugate:
v' = (-t,x,y,z)
We can therefore express the distance scalar as follows:
d = √(v•v')
