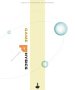
This is an example to show how GA (Geometric Algebra) might be used to simplify the calculations for a solid object collision.
In order to concentrate on the principles rather than the details we will make it as simple as possible while still allowing rotations, Imagine a bar with a length of 1 metre but negligible height or depth. So the shape can be represented by 2 points, vertex 1 and vertex 2 defined as +0.5m and -0.5m in the local co-ordinates of the bar.
The bar is initially 10m above the solid ground and rotating at 0.1 rad/s.
(in the following examples I have not yet done all the calculations properly, I have just made up some of the figures, perhaps we can get the real figures from your program)
So its status at time=0 is as follows:
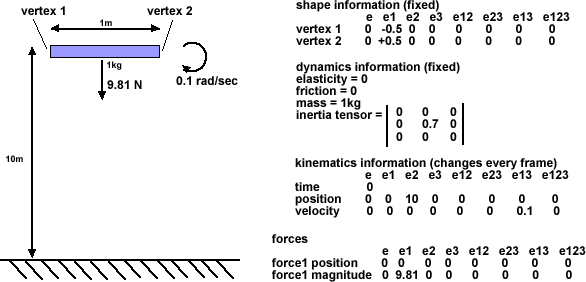
After the first time interval of 0.1 sec the velocity has increased due to gravity but its rotation is constant.
So,
velocity = acceleration + velocity
position = velocity + position
These quantities have both grade 1 and grade 2 components to represent linear and rotational parts.
Although I am happy with adding the rotational component of velocity I am not so happy with adding the rotational component of position (this will only be correct if the change is very small)?
We then check for collisions, to do this we have to calculate the absolute positions of vertex 1 and 2. This involves doing an affine transformation on each vertex at each frame using the position multivector. How do we do such a transform using a multigrade Monad?
We are still well above the ground so no collision is detected. So the situation at time 0.1 is:
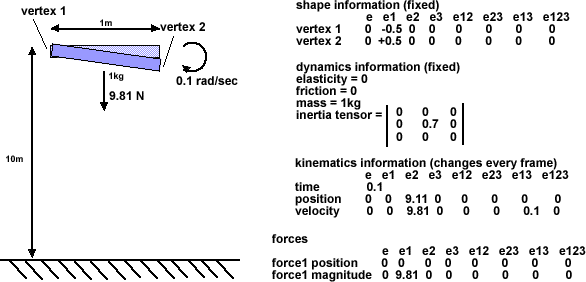
We continue in the same way until we get to the frame just before the collision as follows:

After this, we take one more step and a collision with vertex 2 is detected. In this case the ground is fixed the velocity of the bar will be reversed, but we want to work out the result in a more general way so we calculate Force 2 by averaging out the change in momentum over the time interval.
Although the forces are all grade 1, the total will have a torque component because the forces are acting at different points. So we cant just add the forces or we would loose the torque component, so how do we combine forces to get both linear and rotational component of torque?
The result should reverse the rotation as follows:

Questions so far,
- Is it valid to add rotational parts of position? are there any restrictions that apply to do this?
- How can we use position Monad to do affine transform of verticies?
- How can we add forces to get torque?