Can a free floating object spin in any direction?
A spherical object can rotate in any dimension, but what about an asymmetric object?
To illustrate this, think of a pen or pencil inclined at 45 degrees to the y-axis. If we apply an external torque we can get it to rotate about the y-axis (i.e. at 45 degrees to its long axis). But if we remove the external torque, will it continue to rotate in this way?
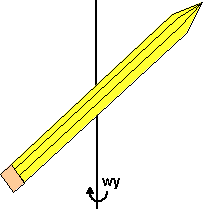
In the interests of science, I have been experimenting an throwing pens in the air. I cant get it to rotate in this way, as soon as it leaves my hand it just wants to rotate about its short axis (i.e. with the pointed end and the erazor on the outside of the spin).
I can get the pen to spin about its short axis or its long axis, but not in-between.
I think I can get it to spin about both these axies at the same time (its difficult to be sure as my eyes aren't fast enough). but what appears to be happening is that it is rotating pointed end over erazor, and then it is spinning about its long axis which is rotating itself. So it appears to be making a complex rotation, as described above, of a rotation within a rotation.
So what are the allowed modes of rotation for any object?
Some answers from Yaakov Eisenberg, thank you for this - Martin : > What if it were being forced to rotate in this direction and then
the external Yes, it would instantly start to rotate about a different axis, but the change is not as discontinuous (therefore, unrealistic) as it might seem. The velocities of the masses change continuously; only their accelerations change discontinuously, due to the discontinuous change in the force. > So given a generalised inertia matrix, what are the conditions for
an object When rotating about the axis, the object's angular momentum vector must be parallel to the axis (i.e., parallel to the object's angular velocity vector). If this is the case, the axis of rotation will remain constant in time. Otherwise, it won't. For any object, there are at least three axes for which this is true. They are called the object's principal axes, and the inertia matrix is diagonal in the coordinate system defined by them. If the object is sufficiently symmetric, there will be more than three. > Is it that single rigid object I think this is also a correct way of stating it. |