Matrix representation
normal component
Norm = Va ![]() P = (Va ×
P) * P/|P|²
P = (Va ×
P) * P/|P|²
This is derived on this page.
parallel component
Proj = Va || P = Va • P * P/|P|²
This is derived on this page.
Reflection matrix
Given the inversion I'll add the terms instead of subtracting them to give the reflection result:
| p -> 1 / (Px² + Py² + Pz²)* |
|
[p] |
Note that this matrix is symmetrical about the leading diagonal, unlike the rotation matrix, which is the sum of a symmetric and skew symmetric part.
Simple cases
In order to check the above lets take the simple cases where the point is reflected in the various axis:
Reflection in yz
| -1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Reflection in xz
| 1 | 0 | 0 |
| 0 | -1 | 0 |
| 0 | 0 | 1 |
Reflection in xy
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | -1 |
Determinant and eigen values
Another check is that the determinant of reflection matrix is -1
Example
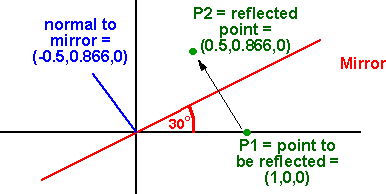
As an example we want to reflect the point (1,0,0) in a plane at 30 degrees.
where Px,Py,Pz is the normal to the mirror which is: (-0.5,0.866,0) and P1 is the initial point which is (1,0,0) substituting these values gives:
multiplying to vector by the matrix gives:
|