Maths - Category Theory - Equivalence

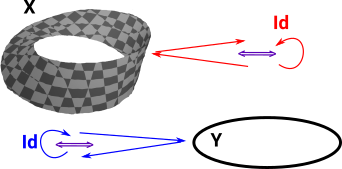
Equivalence As an Isomorphism upto Isomorphism

Equivalence is a relationship between two objects in a similar way to equality and isomorphism but weaker and more general. So isomorphism is weaker than equality and equivalence is weaker (more general) still.

Given two mathematical objects 'C' and 'D' that we want to compare, we construct two morphisms between them 'F' and 'G' as shown in this diagram:
'F' and 'G' must be chosen such that, by applying them one after the other (composing them), we get back to somewhere isomorphic to where we started, That is:
GF1C
FG1D

Equivalence and Subobjects

The concept of a subobject is related to the concept of equivalence.

We can see this in set. If elements are equivalent to some elements and not to others then this partitions the set.

We need to generalise this concept from sets to any category. So we need to externalise the diagram so we have arrows between whole objects.

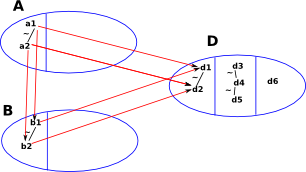As a first step (but still in sets at this stage) we factor set 'A' through set 'B'.

Here I have externalised the diagram so that it is general to any category. The 'dimond' on the head of the arrow indicates that it is monic (never maps distinct objects to the same object).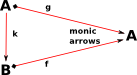
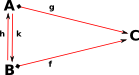
Symmetric This diagram shows that equivalence is symmetric.
Transative This diagram shows that equivalence is transative.
Reflexive This diagram shows that equivalence is reflexive.

Equivalence and Natural Transformations

This raises some questions:

• What does it mean for two morphisms to be isomorphic?
• If isomorphic morphisms are applied to the same domain will the codomains be isomorphic?

One way to define an isomorphism between two morphisms might be to have two natural transformations going each way between them. We will call these natural transformations α and β. That is raise the definitions up a layer.
and again for the other isomorphism. This time with natural transformations γ and δ.

This gives 4 equalities:

• αβ = 1_GF
• βα = 1_1c
• γδ = 1_FG
• δγ = 1_1d

So we start with 1 equivalence, this is defined by 2 isomorphisms, these are defined by 4 equalities.

Equivalence

Better explanation of equivalence on this site.

Example Sets

Sets are don't have duplicate elements, so two different enlements of the same set can't be equal to each other. However we can add an equivalence relation to a set.

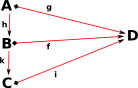
	Here we have a set with 4 elements: A,B,C and D. Suppose we have the following equivalences: A~B C~D
	This is a bit like sets within a set, but where the outside set can 'see' the inside elements.
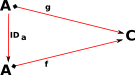
	There is also a more categorical approach to this. We could look at the external properties rather than the internal properties. We could construct a morphism to the equivalence classes.
	We can't construct an inverse to the above morphism (So there is not an isomorphism between these two sets). However we can map back to a set of equivalent values.

The above argument is not quite correct because an equivalence should map back to somewhere isomorphic to the starting point, not equivalent, so its not a proof of the categorical definition of equivalence.

Example Groups

Imagine a group whose structure we will show as a permutation. We will permute 4 elements with two possible permutations (one shown in blue and one in red like this) like this: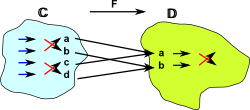
The category 'C' essentially represents the same group as 'D' (that is Z2) so, from the point of view of category theory they are equivalent. That is they have the same behavior. However they are not isomorphic because they have a different number of elements.
The mapping 'F' of the elements from C to D is many (2) to one so when defining the inverse mapping 'G' we have to choose what elements we map back to like this: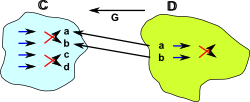

So the round trip GF gives us a copy of C in D.

Equivalence As a Division

If we take function composition as being like multiplication, then the inverse function is like division, and this example does seem to divide C up into parts that are copies of each other.

Weak Equivilance

Weak equivilance gives us a way to do this using only a functor in one direction F. However this only tells us that an equivilance exists, not the functors which give the equivilance. This is discussed on this page.

EuclideanSpace

home

Prerequisites

• Isomorphism

Related Pages

• Non-categorical introduction to equivalence on page here.

Set Symbols

Homotopy Equivalence

If we continuously map every point in X to a point in Y and require an inverse map which brings the point back to where it started and do this in both directions we get a homeomorphism. But if we want a homotopy equivalence (shapes which can be continuously deformed into each other) then we only need a weaker requirement that this round trip and the identity maps are a homotopy.

More about homotopy equivalence on the page here.