Maths - Subgroups and Factoring Groups

Types of 'Division'

On these pages we will discuss these types of 'division' of groups to produce a smaller group:

Subgroup
Quotient Group (or Factor Group)

Quotient groups and subgroups are both ways of forming a smaller group from a larger one. In category theory terms they are duals of each other.

Extension Problem

Unlike conventional multiplication and divisions, where the result of a multiplication can be divided back to give the original operands, these group operations can not always be reversed in this way (although in many cases they can).

An example of where it is not possible is: C4, a cyclic group of order 4, such as complex numbers which can be generated by 'i' which generates the cycle 1->i->-1->-i. We can divide this by C2, for instance '-1' which generates the subgroup 1->-1 . However we cannot reverse this and generate C4 from C2C2 and the semidirect and bicrossed products are identical to the direct product because reversing the direction of arrows in the Cayley graph does not change it.

Subgroup

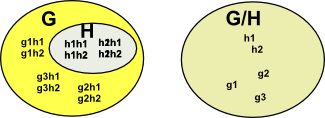
Lets assume that we have a group G and we have a subgroup of G which we call N. We want to find the other subgroup G/N. For G/N to be a group then N must be a normal subgroup. Sometimes, but not necessarily, a group G can be reconstructed from G/N and N, as a direct, semidirect or bicrossed product.

Quotient Group

A quotient group (or factor group) is a group obtained by identifying together elements of a larger group using an equivalence relation.

For example, the cyclic group of addition modulo 5 can be obtained from the integers by identifying elements that differ by a multiple of 5.

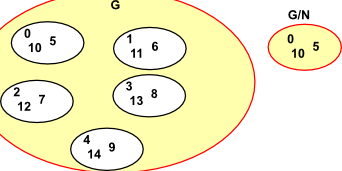
mudulo 5 set

In a quotient of a group, the equivalence class of the identity element is always a normal subgroup of the original group, and the other equivalence classes are the cosets of this normal subgroup. The resulting quotient is written G / N, where G is the original group and N is the normal subgroup.

quotient

Test that N is a normal subgroup

To test that N is a normal subgroup then:

g N g ^-1 must be a member of N for every g in G

Calculation of G/N

we calculate the set:

gN | gG

This will be the group G/N under the operation

(g₁ N) (g₂ N) = g₁ g₂ N

Proof

let H = G/N

to prove that H is a group we must prove that:

H is closed under multiplication	(h₁ N) (h₂ N) = h₁ h₂ N
h^-1 exists	(hN) (h^-1 N) = 1

We will represent multiplication by concatenating into a single word:

(h₁ N) (h₂ N) = h₁ N h₂ N

but since h is an element of G then: h₂N = N h₂

=h₁h₂ N N

Since N is a group it is closed under multiplication. Taking and example element n from N then the produce N N will be n' n

Group Equivalences

The way that left or right cosets of a subgroup partition a group is an equivalence relation. See page here.

let:

H be a subgroup of group G.
~ be an equivalence relation on G
a ~ b ↔ (ab⁻¹H).

	Group	Equivalence Relation
		x~y
transitive	a b^-1b c^-1=a c ^-1 since b^-1b=1	x~y, y~z->x~z (composition law)
reflexive	if a maps to H then composing with 1 wont change that.	x~x
symmetric	The inverse of a b^-1 is b a^-1 If H contains a b^-1 then it must contain its inverse.	x~y->y~x (symmetry law)