Here we look at structure preserving (sometimes called monotone) morphisms between lattices.
In the case of morphisms between lattices we want to preserve meets and joins. So, for example, if:
then we need: a\/b to map to f(a) \/ f(b) that is:
|
 |
So it follows from this that:
- Top (T) maps to top.
- Bottom (
 ) maps to bottom.
) maps to bottom.
If 'a' and 'b' map to the same point then a\/b and a/\b also map to that same point.
 |
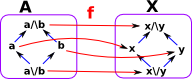
This diagram is an attempt to represent a morphism between two lattices 'X' and 'Y'. The blue arrows are intended to represent the internal structure of the two lattices. The red arrows are intended to represent the morphism between the lattices. So does this mapping correctly preserve the structure? Is it monotone? |
I don't think the above example is valid. For example:
f(a\/b ) ≠f(a) \/ f(b)
That is:
- f(a)=x
- f(b)=y
- f(a\/b)=x
- f(a) \/ f(b)=T
Instead of checking that join and meet are preserved, we could just check the arrows are preserved:
f(a≤b ) = f(a) ≤ f(b)
If we look at the middle arrow of 'X', the top goes to the left branch of 'Y' and the bottom goes to the right branch. However there is no corresponding arrow in 'Y', so the above example does not conserve the structure.
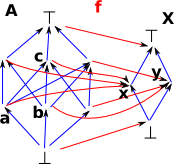
So are there examples, of mappings, that do conserve the structure between these particular lattices? This mapping looks better, as far as I can see, all the rules are obeyed. |
 |
Endomaps
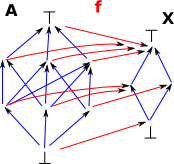
How many structure preserving maps of a lattice back to itself?
If we are mapping the lattice to itself then, the top and bottom elements map to themselves. We seem to be free to permute the next row up from the bottom any way we want, but:
|
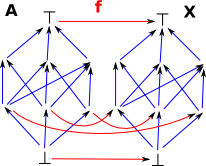 |
However an interesting situation, especially in fixpoint theorems, is when a structure (such as a lattice) maps to a part of itself. As in the diagram on the right: So we create a copy of the lattice inside itself, although some nodes are pushed together. This allows us to model intresting ideas, like recursion. |
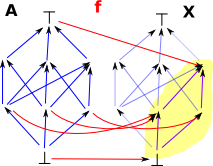 |
Knaster-Tarski Theorem
If L is a complete lattice, then every monotone (i.e., order-preserving) map
f : L -> L has a fixed point
and the fixed points of f form a complete lattice.
For more discussion about fixpoint see page here.
