Maths - Normal Subgroups

If N is a subgroup of G then N is a normal subgroup if:

g N = N g

for all g in G

This does not necessarily mean that g n = n g for all gG, nN but it means that the set {g N} is the same as the set {N g} or, in other words,

g n = n' g

That is, if we choose an n in N then n' will also be a member of N (although not necessarily the same member).

If we multiply the above equation by g^-1 we get:

n' = g n g^-1

where:

• gG
• nN
• n'N

This second form is probably the best way to test if N is a normal subgroup.

Calculation of G/N

we calculate the set:

g N | gG

This will be the group G/N under the operation

(a N) (b N) = a b N

Example 1

Lets take the example of C₃×C₂ :

generator	cayley graph	table
<m,r | m²,r³,rm=mr>		1 r r² m rm r²m r r² 1 rm r²m m r² 1 r r²m m rm m rm r²m 1 r r² rm r²m m r r² 1 r²m m rm r² 1 r

In this example we will test if C₃ is a normal subgroup and then divide by it to check that the result is C₂.

First we need to know the inverse function, to do this we take a particular column, go down until we get to the identity element '1' and then read out the row:

x	x-1
1	1
r	r²
r²	r
m	m
rm	r²m
r²m	rm

let R = the elements of C₃, that is, 1 , r and r²:

x	x 1 x-1	x r x-1	x r² x-1
1	1 1 1 = 1	1 r 1 = r	1 r² 1 = r
r	r² 1 r² = r	r² r r² = r²	r² r² r² = 1
r²	r 1 r = r²	r r r = 1	r r² r = r
m	m 1 m = 1	m r m = r	m r² m = r²
rm	r²m 1 rm = 1	r²m r rm = r	r²m r² rm = r²
r²m	rm 1 r²m = 1	rm r r²m = r	rm r² r²m = r²

So the result is always a member of C₃ so it is a normal subgroup. We can now try divideing by C₃ as follows:

The result of this division has elements R and Rm:

R	Rm
Rm	R

Example 2 - divide C by Z₂

G = Complex numbers = C

N = Z₂

Test for Normal Subgroup

x	x N x-1
1	1 {1,-1} 1 = {1,-1}
-1	-1 {1,-1} -1 = {1,-1}
i	i {1,-1} -i = {1,-1}
-i	-i {1,-1} i = {1,-1}

So x N x^-1 is a member of N for every x which means that G/N will be a group and we can go on to calculate it.

Calculation of G/N

Elements of G/N are a•N:

1•{1,-1} = {1,-1}
-1•{1,-1} = {-1,1}
i•{1,-1} = {i,-i}
-i•{1,-1} = {-i,i}

so the elements are:

{1,-1} and {i,-i}

Example 3 divide H by C

G is the group of quaternions H:

Cayley Table	Cayley Graph
a*b b.1 b.i b.j b.k a.1 1 i j k a.i i -1 k -j a.j j -k -1 i a.k k j -i -1

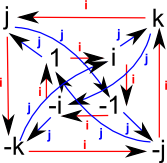Note: in this example I have not shown the negative elements so where i is shown we also have -i and so on for the other elements.

We want to divide it by C to get H/C

Test for Normal Subgroup

x	x K x-1
1	1 {1,i} 1 = {1,i}
i	i {1,i} -i = {-1,-i}
j	j {1,i} -j = {-1,-i}
k	k {1,i} -k = {-1,-i}

So x K x^-1 is a member of K for every x which means that G/K will be a group and we can go on to calculate it.

Calculation of G/N

Elements of G/N are a•N:

1•{1,i} = {1,i}
i•{1,i} = {-1,i}
j•{1,i} = {j,-k}
k•{1,i} = {k,-j}

So the elements are:

{±1,±i} and {±j,±k}

which gives the multipication table:

a*b	{±1,±i}	{±j,±k}
{±1,±i}	{±1,±i}	{±j,±k}
{±j,±k}	{±j,±k}	{±1,±i}

EuclideanSpace

home

 

Rotating a Cube

Generating Geometric Algebras