On this page we give an example for the monoidal categories page. This is especially to illustrate cartesian and tensor products. We could do something similar in categories, although in categories we have the composition of all arrows and the diagrams would be a lot more cluttered, so I have not done that here. However we could think of these graphs as generators for categories.
Cartesian Product
We can extend the concept of cartesian product of sets to categories as follows:
| Here is an ordinary cartesian product of sets. |  |
Here we have sets with structure, represented by arrows. An arrow (a, b) -> (a', b') exists in A×B if and only if either:
|
 |
Tensor Product
We can extend the concept of cartesian product of sets to categories as follows:
The objects are the same as cartesian product of sets but the arrows are different from the cartesian example above. There is an arrow in A An arrow (a, b) -> (a', b') exists in A
|
 |
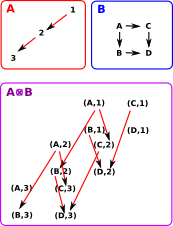Looking at the case above it looks like we could recover projections to A and B from A On the right is a diagram of an extreme case where one of the operands has no arrows. In this case, by the definition given above, the tensor product will have no arrows. In this case there may be a projection from A Perhaps this is an example which shows the cartesian product of graphs is not a product in the category theory sense? |
 |
| A graph with a single object and an arrow to itself is the unit: 1. |  |
B only if there is an arrow in both A and B. Exponential Object
| There is a homset that shows all the ways an object can be mapped into another object: |  |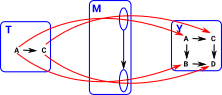
| This is related to the Cartesian product by Currying: | Hom(A×B,C) Hom(A,CB) |
| The related product might look like this: |  |
