Maths - Infinity-Category

n-Categories

This is often described in terms of n-cells. In the diagrams below, the number of lines (shafts) in the arrows indicates the order of the arrow.

0-cell 1-cell 2-cell 3-cell
object arrow arrow between arrows arrow between arrows between arrows
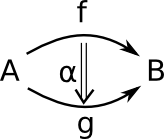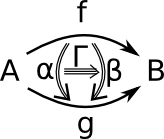0 cell 1 cell 2 cell 3 cell

More about n-categories on this page.

Infinity Categories

In addition to objects and morphisms infinity categories have unlimited higher level morphisms (morphisms between morphisms and morphisms between morphisms between morphisms and so on).

Such categories can be characterised by two numbers (n,k) where:

  • n: is the maximum dimension, in this case ∞.
  • k: the dimension above which all morphisms are invertible.

I am looking at this from a topological point of view. Where a morphisms is invertible this looks like an isomorphism or equivilance but here it may only be upto a homotopy equivalence. That is, there may be many arrows between a given source and target, but they at all related.

Here the most commonly used infinity categories are ( ∞ , 0) and ( ∞ , 1) :

  ( ∞ , 0) category
or
∞-groupoid		 ( ∞ , 1) category
Models for the category: Kan complexes

quasi-category

or
weak Kan complex

More about infinity-categories on this page

 

 

metadata block
see also:

http://stackoverflow.com/questions/13352205/what-are-free-monads
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.
flag flag flag flag flag flag The Princeton Companion to Mathematics - This is a big book that attempts to give a wide overview of the whole of mathematics, inevitably there are many things missing, but it gives a good insight into the history, concepts, branches, theorems and wider perspective of mathematics. It is well written and, if you are interested in maths, this is the type of book where you can open a page at random and find something interesting to read. To some extent it can be used as a reference book, although it doesn't have tables of formula for trig functions and so on, but where it is most useful is when you want to read about various topics to find out which topics are interesting and relevant to you.

 

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2024 Martin John Baker - All rights reserved - privacy policy.