Maths - Concrete Category - Graphs

A step up in complexity from a category of sets we can look at the category of graphs.

Objects in Grf are a collection of vertices and edges related in certain ways. However category theory tends not to look inside objects.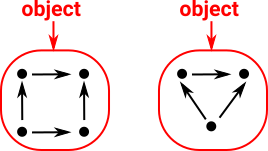
Morphisms in Grf sends vertices to vertices and edges to edges, such that, if a->b is an arrow then F a -> F b is an arrow. Again category theory tends not to look inside these morphisms.

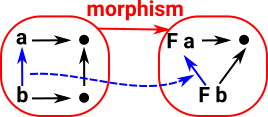Relating Category Theory to Set Theory View of Graphs

So far, on this page, we have drawn graphs as vertices with edges between them. This is a sort of internal view of the graph, category theory gives a more external view.

The category theoretic approach is to investigate objects, in this case graphs, in terms of the arrows (morphisms) between objects. So we are probing it from the outside.

The internal view can be more intuitive, especially to newcomers to category theory, so here we are relating the internal and external views to help with intuition. A graph is similar to a category theory diagram, but is weaker, in the sense that there is no requirement for compositions and identity loops to exist. Although category theory diagrams and graphs are different in this way here we see how they interact so we can get some information about the graph from its category theory diagram.

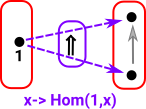
To do this we need to work with all the arrows from an object so we need to have the concept of a homset (see page here)

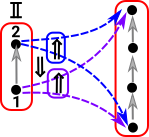
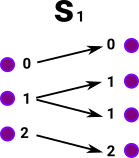
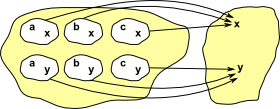
As a start with this approach we want to probe the red object on the right: To do this start by 'probing' it with arrows from a graph with only one vertex and no edges. All the possible arrows from the single vertex object form a homset. This homset is a set (where the elements are arrows) so we can use our set theoretic intuition on it. This set has one object for every vertex in the object.

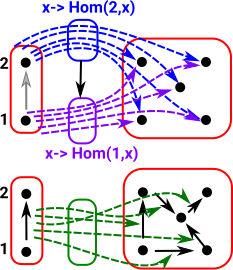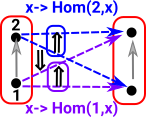
Now we need to 'probe' the edges. We can do this with an arrow from a graph with a single edge between two vertices. The bottom part of the graph on the left shows arrows (green) to each edge. So this time we have a homset which gives the number of edges. However, the mapping of the edges needs to play well with the mapping of the vertices (top part of diagram). The set of arrows from vertex 1 is covariant x -> Hom(1,x) : Grf -> Set this is usually written Hom(1,_) Similarly with vertex 2 x -> Hom(2,x) : Grf -> Set However the mapping between these two sets Hom(2,_) -> Hom(1,_) is contravarient (it goes down on the diagram where the other mappings go up).

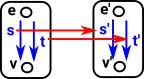
It is easier to see this contravarience from a simpler diagram. If 'F' is given we can derive 'h' from 'g' by composing with 'F' but we can't derive 'g' from 'h'. So if we want to get the usual functions in set we need to start with Grfop A contravarient functor of the form Cop->set occurs in other structures and is called a presheaf as described on page here.

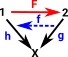This graph object that we are using to 'probe' another graph object is known as a representable object in Grf (see Yoneda lemma page). This representable object is a graph with two vertices and an arrow between them.

• More about relating category theory to set theory view of graphs on page here.
• We can extend this example from graphs to simplicial sets as described on page here.

Gluing

We have a contravarient functor which picks out edges but the edges are not all separate so how do we encode this additional structure?

The edges are connected when they share a common point.

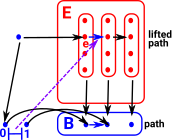In order to understand this we need the concepts of fibration and lifting as described on the page here.

Paths

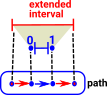
What happens when there are a sequence of edges following each other? (the target of the first is equal to the source of the second and so on). Can the edge in the interval match the whole path? Is this the same thing as requiring composition?

In order to understand this we need the concepts of cofibration and extentions as described on the page here.

Grf^op

Objects in Grfop are the same as the objects in Grf.
Morphisms in Grfop go in the opposite direction to the morphisms in Grf. So this time: if F a-> F b is an arrow then a -> b is an arrow.

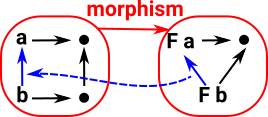In Grf these functions can be surjective or injective as with set.	surjective function
	injective function
In Grfop these arrows can be the reverse of these.

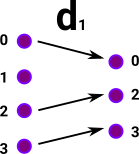So this embedding is given by:

h_X = hom_C(_,X) : Grf ^op-> Set

Internal View

Although category theory does not tend to look inside objects it is helpful to relate this to a more set theoretical approach.

The objects in Grf consist of a set together with some internal structure.

Directed Graph

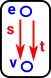Two functions, source and target) from the set of edges to the set of vertices.

Two functions, between the source and target objects, which respect the graph structure.

An example of a functor category.

These maps between the source and target imply functors of the verticies and edges. So what does it mean for the arrows to respect the graph structure? For instance, if we look inside the functions, the diagram on the right is valid.
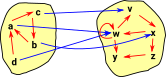If we look at parts of this arrow we see: edges map to edges
Where the vertex function is surjective edges may be reduced to a loop.
Both the vertex function and the edge function may be injective.

Functors Between Graphs

Lets look at the possible diagrams for graphs.

	External diagram	Internal mapping for a specific example
category diagram: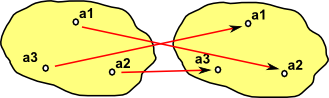
simpler diagram which we can use in the case of endomaps: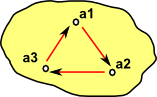

An endomap is a mapping from a object to itself. A category diagram for this case is shown in the higher row in the table above, we can see that it is an endomap because both the domain and the codomain are labled 'A', and hence are the same.

However, because this is an endomap, we can simplify the diagram by showing 'A' as one object.

Graph Categories

So lets start with Grf, a category of graphs, these have a bit more structure than sets and so will allow us to explore the relationships between objects which are sets+structure. I find it helpful to adapt the diagrams as bit, to get us started, so that we can include some of the normally hidden structure beneath. This is just to get us started, we won't always do this as the nature of category theory is to abstract as much as possible. Lets start with sets, which are perhaps the simplest objects, because they don't have the structure of operations like multiplications and additions.

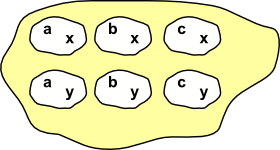	Sets may just be any set of elements, or some or all of these sets may themselves be sets (and these inner sets may also contain sets and so on). Also these elements may all have a common type or not. So we could show the structure inside the set instead of representing them as single characters.
	In the case of structures like groups with a group operation then we could show that, perhaps by combining with a Cayley graph.

Arrows

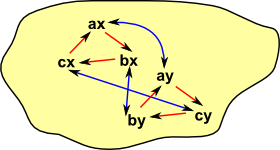
I find that including this further information helps even more with arrows:

	Here I have showed individual arrows going from each element of the two objects rather than the more usual single arrow between the two objects.
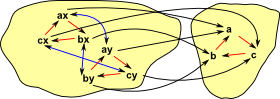	In the case of groups we may be able to give an indication of how the group operation is changed by the arrow.

We will call the object at the start of the arrow the 'domain' and the object at the end of the arrow the 'codomain'

Subcategories of Grf

Two important subcategories are idempotent and invertible endomaps:

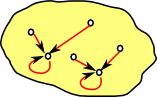	Idempotent Endomap All arrows lead to fixed points.
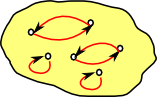	Invertible Endomap (permutation). contains only 2-cycles and fixed points

Grf^op

The dual of graph is a category with the same objects as Grf but with the arrows reversed.

normal function The blue arrows are intended to show inside an arrow between two grf objects. Multiple vertices can be compressed down to a single point (surjective), for example, 'a' and 'b' both map to 'w'. Some vertices in the codomain don't have incoming arrows, for example, 'y' and 'z'.
reversed function When the arrows are reversed it is possible for a vertex, for example, 'w' to be mapped to multiple vertices 'a' and 'b'.

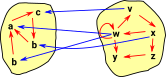That defines Grf^op but it would be better if the revered arrow behaved like a function, that is, if we could change the structure of the objects instead of the arrows (as we did for sets on page here).

Is this possible?

Irriflexive Graphs

Endomaps (mappings from an object to itself) are related to two parallel maps between different objects.

	External diagram	Internal mapping for a specific example
Irriflexive Graph: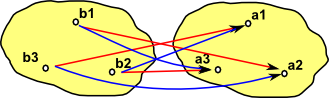
related endomap:

The endomap is given by the difference between the red and blue mappings.

Adjunctions in Graphs

Adjunctions in Graphs

Adjunctions are described on page here.

Between reflexive graph and set. In reflexive graph: every node has loop to itself.

Between irreflexive graph and set. In irreflexive graph: every node does not have loop to itself.

Between dynamical system graph and set. In dynamical system graph: every node has one outgoing arrow.

Different dynamical system graph and set. This time the morphism to set defines the fixpoints.

Exponential Objects in Graph

There is a homset that shows all the ways an object can be mapped into another object: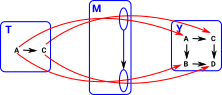
This is related to the Cartesian product by Currying:	Hom(A×B,C)Hom(A,CB)
The related product might look like this:

See page here about Cartesian Closed Category structures in graphs.

Monoid

If we overlay multiple graphs (shown in different colours) then we get a Cayley graph as discussed on this page. This gives us a way to move onto monoids and groups in terms of category theory on this page.

Next

See page here about Cartesian Closed Category structures in graphs.

 

EuclideanSpace

home

This page discusses how category theory represents and uses graphs, for a more set theory like introduction to graph theory goto this page:

• Graph Theory

As an aside graphs are related to category theory diagrams. Category theory diagrams are directed graphs with Id arrows and composition of arrows.

Set Symbols

Functional Programming and Category Theory

Category Theory