Monoids and Groups are categories with one object and an (endo-)functor going from that single functor back to itself. So this is the simplest type category that still has some structure. This is useful to study because:
|
| In the diagram we have a 3 layer hierarchy, at the top we have a node representing all sets. Below that we have various types of sets such as, the empty set, a set with one element, a set with two elements and so on. Below that we have the elements of the sets. | 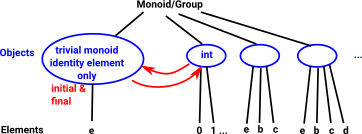 |
Category theory concentrates on the middle of these 3 layers. That is, we do not derive properties by looking inside at the elements of the sets, instead we derive properties by looking at the mapping between sets.
In Set theory Terms
First a reminder of the conventional set theory approach to these structures.
A monoid is a semigroup with an identity element or a group without inverse (these group-like structures are discussed in conventional terms on these pages).
 |
The axioms required of a monoid operation are those required of morphism composition when restricted to the set of all morphisms whose source and target is a given object. A monoid is a category with a single object. Given a monoid (M,*), one can construct a small category with only one object and whose morphisms are the elements of M. The composition of morphisms is given by the monoid operation *. |
Cayley's theorem states that every group is isomorphic to a subgroup of the symmetric group on G. That is to set of permutations or endo-mappings where the multipication operation is functional composition of these endo-mappings.
Endomap
When we looked at graphs we saw how an endomap is represented. If we overlay several graphs (shown here as red and blue) we get a Cayley graph.
| External diagram | Internal mapping for a specific example | |
|---|---|---|
| category diagram: | 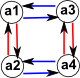 |
So a single object with maps to itself can be a monoid but this does not really tell us much about the internal structure of the monoid/group.
Group in Category Theory Terms
In set theory terms we looked at a group as a set+structure, here we want to define this structure by its external properties (that is in terms of structure preserving mappings: functors) which is a more category theoretical approach and has the advantage that we can define it over structures other than sets.
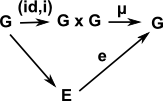
How can we relate this to the structure in terms in the group identities:
We define:
- a multipication mapping: μ: G×G -> G
- an inverse mapping: i: G -> G
- a identity mapping: e: * -> G (where * = a terminal set)
Axioms:
| Set Theory | Category Theory | |
|---|---|---|
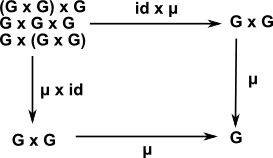
| Associatively | (a b) c = a (b c) | μ•(id×μ) = μ•(μ×id) |
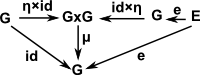
| Identity element (unit) | 'e' such that: e a = a = a e | μ•(η×id) = id = μ•(id×η) |
| Inverse element | 'a-1' such that: a a-1 = e = a-1 a | μ•(id×δ)•Δ = η•ε = μ•(δ×id)•Δ |
where:
- μ: G×G -> G = multiplication
- δ: G -> G = a->a-1 = inverse
- η: G -> * = e = unit
- With the following two additions which only work where the monoidal product is the carteasian product (this is true in groups/moniods over sets for example)
- ε: * -> G
- Δ: G -> G×G = a->(a,a) = diagonal
These category theory axioms are derived from the set theory versions as follows,
- First we express them in terms of the internal set elements a,b and c.
- Then we move (a,b,c) to the right and the operators (mappings) to the left.
- Then, since the set elements are the same on both sides of the equation, we can cancel them out and express the axioms purely in terms of the mappings.
| Group Associativity |
μ(a,μ(b,c)) = μ(μ(a,b),c) μ(id×μ)(a,b,c) = μ(μ×id)(a,b,c) μ•(id×μ) = μ•(μ×id) |
 |
| Group Identity (unit) |
μ(e×a) = a = μ(a×e) μ•(η×id) = id = μ•(id×η) |
 |
| Group Inverse |
|
 |
We discuss this idea of taking a group and extracting the structure from the underlying set on this page.
Natural Numbers
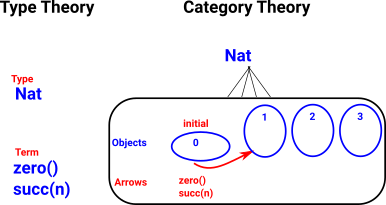 |
Lists Form a Free Monoid

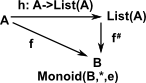 |
Lists form a free monoid, that is, this diagram commutes. |
This concept can be extended to other free structures see [R.M. Burstall and P.J. Landin, "Programs and their proofs, an algebraic approach", Machine Intelligence 4(1969)]
more about lists on this page.
Universal Properties of Monoid or Group
See this page for a discussion of universal properties.
| Terminal | Initial |
|---|---|
 |
 |
| trivial monoid (consisting of only the identity element) | trivial monoid |
| Product (pullback) |
Sum |
|---|---|
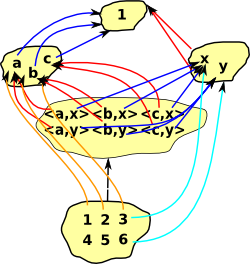 |
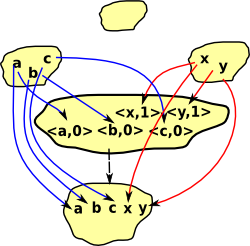 |
| the product is given by the cartesian product with multiplication defined componentwise. | free product the free product for groups is generated by the set of all letters from a similar "almost disjoint" union where no two elements from different sets are allowed to commute. |
