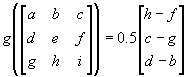Maths - Matrix Calculus

Prerequisites

If you are not familiar with matrix algebra you may like to look at the following pages first:

In the applications section it is important to realise there are different standards and conventions and therefore it is a good idea to familarise yourself with the standards used on this site:

Matrix differentiation

To differentiate a matrix with respect to a variable, say 'x', we individually differentiate each element with respect to 'x'. So if:

[f(x)]=
f00(x) f01(x) f02(x)
f10(x) f11(x) f12(x)
f20(x) f21(x) f22(x)

then:

[ d f(x) / dx]=
d f00(x) / dx d f01(x) / dx d f02(x) / dx
d f10(x) / dx d f11(x) / dx d f12(x) / dx
d f20(x) / dx d f21(x) / dx d f22(x) / dx

So to give a more specific example if:

[f(x)]=
xn sin(x) tan(x)
ex x2 x3
cos(x) 3 0

then:

[ d f(x) / dx]=
n*xn-1 cos(x) sec2(x)
ex 2*x 3*x2
-sin(x) 0 0

So this is quite simple, provided that we can differentiate the elements of a matrix, we can differentiate the whole matrix.

Matrix Differentiation with respect to another Matrix

Since division of one square matrix, with non-zero determinant, by another will give a result (unlike vectors) we can define differentiation with respect to another matrix.

What are the rules of such differentiation? What applications does it have?

gears

Could we use it in this situation? Imagine that two matrices represent the angular position of two gears, can we differentiate one with respect to another to get the ratio of the gears?

Jacobian matrix

There are more complicated types of differentiation, for instance the Jacobian which gives all combinations of the partial differentials of elements of the vector with the other elements.

J (x1,x2...xn) =
d y1 / dx1 ... d y1 / dxn
... ... ...
d yn / dx1 ... d yn / dxn

This is related to vector calculus such as grad, div and curl.

Applications

Here we are considering the simple differentiation of a matrix at the top of this page. However, when we start to look at applications it becomes less simple.

For instance, with linear movement we just use v = dx/dt and we treat velocity v as being the same thing as dx/dt but with rotation the equation is more complicated: 
[~w]*[R(t)] = [d R(t) / dt] 

This is also discussed on the angularvelocity page and in particular Mark Ioffe was kind enough to send me a proof of this, see this page.
 
What I want to do is understand the deeper reasons for this extra complexity. I think this involves these factors:

Two Dimensional Case

Rotation matrix is: [R]=
cos(a) -sin(a)
sin(a) cos(a)

We want the object to be rotating at a constant angular velocity of 'w'. Therefore we replace the angle 'a' with w*t as follows:

Rotation matrix is: [R]=
cos(wt) -sin(wt)
sin(wt) cos(wt)

So if we differentiate this with respect to time we get:

d[R] / d t=
-w*sin(wt) -w*cos(wt)
w*cos(wt) -w*sin(wt)

So, as already described, this is a time varying quantity even though it is rotating at a constant angular velocity. However we can factor this matrix as follows:

-w*sin(wt) -w*cos(wt)
w*cos(wt) -w*sin(wt)
=
0 -w
w 0
*
cos(a) -sin(a)
sin(a) cos(a)

so if we let

[~w] =
0 -w
w 0

Then we get:

[d R(t) / dt] = [~w]*[R(t)]

So we now have a non-time-varying matrix to represent angular velocity.

Three Dimensional Case

If

a(t)= [R(t)]l

where:

In other words, if we take a fixed point on an object, and transform the object by multiplying it with a rotation matrix, which is a function of time, then we will get a vector which is rotating as defined by the matrix.

If we want to get the velocity of this vector then we need to differentiate the matrix t give,

a(t)= [(t)]l

where:

We want to prove that: (t)=[~w] R(t)

In other words that:

(t)=
0 -wa wh
wa 0 -wb
-wh wb 0
R(t)

R(t) can be expressed in terms of euler angles (as explained on this page)

(t)=
0 -wa wh
wa 0 -wb
-wh wb 0
ch*ca -ch*sa*cb + sh*sb ch*sa*sb + sh*cb
sa ca*cb -ca*sb
-sh*ca sh*sa*cb + ch*sb - sh*sa*sb + ch*cb

 

(t)=
-wa*sa - wh*sh*ca -wa*ca*cb + wh*sh*sa*cb + wh*ch*sb wa*ca*sb - wh*sh*sa*sb + wh*ch*cb
wa*ch*ca- wb*sh*ca -wa*ch*sa*cb + wa*sh*sb + wb*sh*sa*cb + wb*ch*sb wa*ch*sa*sb + wa*sh*cb - wb*sh*sa*sb + wb*ch*cb
-wh*ch*ca + wb*sa wh*ch*sa*cb -wh*sh*sb + wb*ca*cb -wh*ch*sa*sb -wh*sh*cb - wb*ca*sb

Assume that we have a matrix representing the position and orientation of a solid object, this transforms relative coordinates into global coordinates as follows,

[point in global coordinates]=
m00 m01 m02
m10 m11 m12
m20 m21 m22
[point in relative coordinates]

This matrix can be expressed in terms of euler angles (as explained on this page) using standard aeroplane conventions:

ch*ca -ch*sa*cb + sh*sb ch*sa*sb + sh*cb
sa ca*cb -ca*sb
-sh*ca sh*sa*cb + ch*sb - sh*sa*sb + ch*cb

where:

  • ch = cos(heading)
  • sh = sin(heading)
  • heading = rotation about y
  • ca = cos(attitude)
  • sa = sin(attitude)
  • attitude = angle about z (applied second)
  • cb = cos(bank)
  • sb = sin(bank)
  • bank= angle about x (applied last)

So we can get the rate of change of the point by differentiating the matrix:

[d(point in global coordinates)/dt]=
d(m00)/dt d(m01)/dt d(m02)/dt
d(m10)/dt d(m11)/dt d(m12)/dt
d(m20)/dt d(m21)/dt d(m22)/dt
[point in relative coordinates]

So in terms of angles this gives:

[dR/dt] =
d(ch*ca)/dt -d(ch*sa*cb)/dt+d(sh*sb)/dt d(ch*sa*sb)/dt+d(sh*cb)/dt
d(sa)/dt d(ca*cb)/dt -d(ca*sb)/dt
-d(sh*ca)/dt d(sh*sa*cb) /dt+ d(ch*sb)/dt -d(sh*sa*sb)/dt+d(ch*cb)/dt

using the following differention rules:

  • d(x*y) = x d(y) + y d(x)
  • d sx / dt = d sx / dx * d x / dt = cx * wx
  • d cx= / dt = d cx / dx * d x / dt = -sx * wx

therefore d(x*y)/t = x wy + y wx

where wx = angular velocity about x

so this gives:

d(cx cy) = cx d(cy) + cy d(cx) = - cx sy wy - cy sx wx

d(sx cy) = sx d(cy) + cy d(sx) = -sx sy wy + cy cx wx

d(cx sy) = cx d(sy) + sy d(cx) = cx cy wy - sy sx wx

d(sx sy) = sx d(sy) + sy d(sx) = sx cy wy + sy cx wx

d(cx sy cz) = cx sy d cz + d(cx sy) cz = - cx sy sz wz + cx cy cz wy - sy sx cz wx

d(cx sy sz) = cx sy d sz + d(cx sy) sz = cx sy cz wz + cx cy sz wy - sy sx sz wx

d(sx sy cz) =

[dR/dt] =
- ch * sa * wa - ca * sh * wh - ch sa sb wb + ch ca cb wa - sa sh cb wh + sh cb wb + sb ch wh ch sa cb wb + ch ca sb wa - sa sh sb wh -sh sb wb + cb ch wh
ca * wa - ca sb wb - cb sa wa -ca cb wb + sb sa wa
sh * sa * wa - ca * ch * wh    

This does not seem to be giving the right answer, can anyone see what I'm doing wrong?

Try this with global euler angles:

We want to prove that: (t)=[~w] R(t)

In other words that:

(t)=
0 -wz wy
wz 0 -wx
-wy wx 0
R(t)

R(t) can be expressed in terms of euler angles (as explained on this page)

(t)=
0 -wz wy
wz 0 -wx
-wy wx 0
cy * cz sx*sy*cz-cx*sz cx*sy*cz+sx*sz
cy * sz sx*sy*cz +cx*cz cx*sy*sz-sx*cz
-sy sx*cy cx*cy

 

(t)=
-wz*cy*sz - wy*sy -wz*sx*sy*cz -wz*cx*cz + wy*sx*cy -wz*cx*sy*sz+wz*sx*cz + wy*cx*cy
wz*cy*cz + wx*sy wz*sx*sy*cz-wz*cx*sz-wx*sx*cy wz*cx*sy*cz+wz*sx*sz-wx*cx*cy
-wy*cy*cz + wx*cy*sz -wy*sx*sy*cz+wy*cx*sz -wy*cx*sy*cz-wy*sx*sz + wx*cx*sy*sz-wx*sx*cz

Assume that we have a matrix representing the position and orientation of a solid object, this transforms relative coodinates into global coordinates as follows,

[point in global coordinates]=
m00 m01 m02
m10 m11 m12
m20 m21 m22
[point in relative coordinates]

This matrix can be expressed in terms of euler angles (as explained on this page) using standard aeroplane conventions:

cy * cz sx*sy*cz-cx*sz cx*sy*cz+sx*sz
cy * sz sx*sy*cz +cx*cz cx*sy*sz-sx*cz
-sy sx*cy cx*cy

where:

  • ch = cos(heading)
  • sh = sin(heading)
  • heading = rotation about y
  • ca = cos(attitude)
  • sa = sin(attitude)
  • attitude = angle about z (applied second)
  • cb = cos(bank)
  • sb = sin(bank)
  • bank= angle about x (applied last)

So we can get the rate of change of the point by differentiating the matrix:

[d(point in global coordinates)/dt]=
d(m00)/dt d(m01)/dt d(m02)/dt
d(m10)/dt d(m11)/dt d(m12)/dt
d(m20)/dt d(m21)/dt d(m22)/dt
[point in relative coordinates]

So in terms of angles this gives:

[dR/dt] =
d(cy * cz)/dt d(sx*sy*cz)/dt-d(cx*sz)/dt d(cx*sy*cz)/dt+d(sx*sz)/dt
d(cy * sz)/dt d(sx*sy*cz)/dt+d(cx*cz)/dt d(cx*sy*sz)/dt-d(sx*cz)/dt
-d(sy)/dt d(sx*cy) /dt d(cx*cy)/dt

using the following differention rules:

  • d(x*y) = x d(y) + y d(x)
  • d sx / dt = d sx / dx * d x / dt = cx * wx
  • d cx= / dt = d cx / dx * d x / dt = -sx * wx

therefore d(x*y)/t = x wy + y wx

where wx = angular velocity about x

so this gives:

d(cx cy) = cx d(cy) + cy d(cx) = - cx sy wy - cy sx wx

d(sx cy) = sx d(cy) + cy d(sx) = -sx sy wy + cy cx wx

d(cx sy) = cx d(sy) + sy d(cx) = cx cy wy - sy sx wx

d(sx sy) = sx d(sy) + sy d(sx) = sx cy wy + sy cx wx

d(cx sy cz) = cx sy d cz + d(cx sy) cz = - cx sy sz wz + cx cy cz wy - sy sx cz wx

d(cx sy sz) = cx sy d sz + d(cx sy) sz = cx sy cz wz + cx cy sz wy - sy sx sz wx

d(sx sy cz) =

[dR/dt] =
- cy sz wz - cz sy wy    
cy cz wz - sz sy wy    
-cy * wy    

This does not seem to be giving the right answer, can anyone see what I'm doing wrong?

 

Try this with global euler angles:

We want to prove that: (t)=[~w] R(t)

In other words that:

(t)=
0 -wz wy
wz 0 -wx
-wy wx 0
R(t)

R(t) can be expressed in terms of euler angles (as explained on this page)

(t)=
0 -wz wy
wz 0 -wx
-wy wx 0
cy * cz cy * sz -sy
sx*sy*cz - cx*sz sx*sy*sz + cx*cz sx*cy
cx*sy*cz + sx*sz cx*sy*sz - sx*cz cx*cy

 

(t)=
-wz*sx*sy*cz + wz*cx*sz + wy*cx*sy*cz + wy*sx*sz -wz*sx*sy*sz - wz*cx*cz + wy*cx*sy*sz - wy*sx*cz -wz*sx*cy + wy*cx*cy
wz*cy*cz - wx*cx*sy*cz - wx*sx*sz wz*cy*sz - wx*cx*sy*sz + wx*sx*cz -sy*wz -wx*cx*cy
-wy*cy*cz + wx*sx*sy*cz - wx*cx*sz -wy*cy*sz + wx*sx*sy*sz + wx*cx*cz wy*sy + wx*sx*cy

Assume that we have a matrix representing the position and orientation of a solid object, this transforms relative coodinates into global coordinates as follows,

[point in global coordinates]=
m00 m01 m02
m10 m11 m12
m20 m21 m22
[point in relative coordinates]

This matrix can be expressed in terms of euler angles (as explained on this page) using standard aeroplane conventions:

cy * cz cy * sz -sy
sx*sy*cz - cx*sz sx*sy*sz + cx*cz sx*cy
cx*sy*cz + sx*sz cx*sy*sz - sx*cz cx*cy

where:

  • ch = cos(heading)
  • sh = sin(heading)
  • heading = rotation about y
  • ca = cos(attitude)
  • sa = sin(attitude)
  • attitude = angle about z (applied second)
  • cb = cos(bank)
  • sb = sin(bank)
  • bank= angle about x (applied last)

So we can get the rate of change of the point by differentiating the matrix:

[d(point in global coordinates)/dt]=
d(m00)/dt d(m01)/dt d(m02)/dt
d(m10)/dt d(m11)/dt d(m12)/dt
d(m20)/dt d(m21)/dt d(m22)/dt
[point in relative coordinates]

So in terms of angles this gives:

[dR/dt] =
d(cy * cz)/dt d(cy * sz)/dt -d(sy)/dt
d(sx*sy*cz)/dt-d(cx*sz)/dt d(sx*sy*sz)/dt+d(cx*cz)/dt d(sx*cy)/dt
d(cx*sy*cz)/dt+d(sx*sz)/dt d(cx*sy*sz)/dt-d(sx*cz)/dt d(cx*cy)/dt

using the following differention rules:

  • d(x*y) = x d(y) + y d(x)
  • d sx / dt = d sx / dx * d x / dt = cx * wx
  • d cx= / dt = d cx / dx * d x / dt = -sx * wx

therefore d(x*y)/t = x wy + y wx

where wx = angular velocity about x

so this gives:

d(cx cy) = cx d(cy) + cy d(cx) = - cx sy wy - cy sx wx

d(sx cy) = sx d(cy) + cy d(sx) = -sx sy wy + cy cx wx

d(cx sy) = cx d(sy) + sy d(cx) = cx cy wy - sy sx wx

d(sx sy) = sx d(sy) + sy d(sx) = sx cy wy + sy cx wx

d(cx sy cz) = cx sy d cz + d(cx sy) cz = - cx sy sz wz + cx cy cz wy - sy sx cz wx

d(cx sy sz) = cx sy d sz + d(cx sy) sz = cx sy cz wz + cx cy sz wy - sy sx sz wx

d(sx sy cz) =

[dR/dt] =
- cy sz wz - cz sy wy    
     
     

This does not seem to be giving the right answer, can anyone see what I'm doing wrong?

 

A

 

An example

object rotating about the x-axis with an angular velocity of wx

R(t)=
1 0 0
0 cos(wx t) -sin(wx t)
0 sin(wx t) cos(wx t)

So if we differentie this matrix with respect to time (by individually differentiating each element) we get:

(t)=
1 0 0
0 - wx sin(wx t) - wx cos(wx t)
0 wx cos(wx t) - wx sin(wx t)

Notice that this is just R(t) but mutiplied by wx and rotated by 90 degrees. So we can seperate out these factors as follows:

(t)=
0 0 0
0 0 -wx
0 wx 0
1 0 0
0 cos(wx t) - sin(wx t)
0 sin(wx t) cos(wx t)

So in this case we can differentiate R(t) to give (t) just by multiplying by a constant (not a function of time) matrix.

 

What if the object is rotating about the y axis, in this case,

y(t)=
0 0 wy
0 0 0
-wy 0 0
cos(wy t) 0 - sin(wy t)
0 1 0
sin(wy t) 0 cos(wy t)

 

What if the object is rotating about both the x axis and the y axis, in this case we can use the following identity,

d/dt (YZ) =X * d/dt (Y) + d/dt (X) * Y

to give,

y(t)= Rx(t) * y(t) + x(t) * Ry(t)

(t)=
1 0 0
0 cos(wx t) -sin(wx t)
0 sin(wx t) cos(wx t)
0 0 wy
0 0 0
-wy 0 0
cos(wy t) 0 - sin(wy t)
0 1 0
sin(wy t) 0 cos(wy t)
+
0 0 0
0 0 -wx
0 wx 0
1 0 0
0 cos(wx t) - sin(wx t)
0 sin(wx t) cos(wx t)
cos(wy t) 0 - sin(wy t)
0 1 0
sin(wy t) 0 cos(wy t)

So,

(t)= Rx(t)
0 0 wy
0 0 0
-wy 0 0
Ry(t) +
0 0 0
0 0 -wx
0 wx 0
Rx(t)Ry(t)

I was hoping to show that,

(t)=
0 0 wy
0 0 -wx
-wy wx 0
R(t)

But I cant work out how to get there can anyone help?

and if the object is rotating about all 3 axis then:

(t)=
0 -wz wy
wz 0 -wx
-wy wx 0
R(t)

(t)=[~w] R(t)

 

Derivation of

Maths - Matrix Calculus

Reginald E. Bednar

January 26, 2004

Notation:

Form inertial to body coordinate transformation matrix and its inverse:

Use fact that position vector in body frame is a constant:

Form body frame unit vectors in inertial frame coordinates:

For derivative of body frame unit vectors in inertial frame coordinates:

Express inertial to body coordinate transformation matrix and derivative with respect to time of body to inertial coordinate transformation matrix in terms of these vectors:

The relationship between a unit vector and its time derivative is given by:

Expressing this relationship in the body frame, this yields:

Using above, substituting (1,0,0), (0,1,0), and (0,0,1) successively for , get:

Noting that unit vectors in body frame are:

Want to compute:

Body frame unit vectors are related to each other by:

Now resolve each element of matrix:

Express the body rotation rate in terms of inertial frame coordinates:

Resulting in the matrix in terms of rates:

Thus this matrix is a function of the body rotation rate vector expressed in inertial frame coordinates. This vector is typically not used in applications; the expression using the body rotation rate vector expressed in body frame coordinates is used instead. The latter vector is directly obtained from inertial measurement unit data, i.e., from rate gyros.

 

 

 

 

Dan Piponi (rotations@sigfpe.com) has kindly sent me information about this, here:

If you rotate a vector by a small angle around an axis then the rotation can be written approximately as

('x' is the cross product)

where:

w is a vector in the direction of the axis of rotation and the length of the vector is the size of the angle (in radians) (lets call this the 'rotation vector').
To prove this use the fact that for small angles, a, sin(a) is approximately a and do some basic trig.

Now define the function f(.) that converts vectors into skew-symmetric matrixes by:

Then it's easy to show by writing out components that w x v is f(w)v - ie.
doing a cross product with w is the same as multiplying by a certain matrix.

Define the 'inverse' function on matrices g(.) so that

So g(f(w))=w (though f(g(A))=A is only true if A is antisymmetric).

So now we can say that rotation around axis w by angle |w| is given by the matrix 1+f(w) for small |w|.

So suppose at time t the orientation of something is given by matrix A(t).
Then the change from t to t+dt must be a small rotation. In other words

A(t+dt)=(1+f(wdt))A(t) for small dt

where w is the angular velocity. (I hope you get that the rotation vector, for small dt, is given by wdt)

So f(w) = (A(t+wdt)A(t)^(-1) - 1)

Hence w is g(A(t+wdt)A(t)^(-1) - 1)

So

w = lim g(A(t+wdt)A(t)^(-1)-1)/dt as dt->0

Now A(t+wdt) is, to first order, A+wdt dA/dt. By dA/dt I mean simply the derivative of A with respect to time where you simply differentiate each element of the matrix with respect to time.

So now we get

w = g(dA/dt A^(-1))

Simple eh?

Let's do an example. Consider the matrix

 

At t = 0



So w = (0 0 1).

We already know that the matrix A defines rotation about the z-axis so this is correct. I'll leave you to check the calculation at general t - you should get the same result as A corresponds to constant angular velocity.

I've never actually seen this discussed in any textbook although if you generalise a bit this is an example of Lie algebra theory which is in many books. The operations f and g are sometimes known as the Hodge dual and are written as '*'.

A completely different approach to differentiating rotations is via geometric algebra and rotors. I don't see the need though as I think the above approach is fine. In fact I've used the above approach to differentiating rotations for finding minima and maxima of functions of rotations at work - traditionally the type of problem for which people use geometric algebra. But check the subject out anyway - search on 'geometric algebra hestenes' at google.com.

Have you ever studies the 'spinning top' mathematically? If you have you may spot the connection between the above and the differential equation dv/dt = w x v

Tell me what doesn't make sense!
--
Dan

Matrix integration

As with differentiation we can integrate a whole matrix by individually integrating each element. So if:

[f(x)]=
f00(x) f01(x) f02(x)
f10(x) f11(x) f12(x)
f20(x) f21(x) f22(x)

then:

[ intergral f(x) dx]=
intergral f00(x) dx intergral f01(x) dx intergral f02(x) dx
intergral f10(x) dx intergral f11(x) dx intergral f12(x) dx
intergral f20(x) dx intergral f21(x) dx intergral f22(x) dx
metadata block
see also:

quaternion equivalent of this
Correspondence about this page Forum Discussion with Tadd

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

 

cover Multivariable Calculus with Matrices

Commercial Software Shop

Where I can, I have put links to Amazon for commercial software, not directly related to the software project, but related to the subject being discussed, click on the appropriate country flag to get more details of the software or to buy it from them.

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.