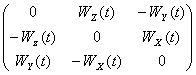In a previous discussion about quaternion differentiation I suggested that it would be interesting to follow the same method, but use orthogonal matrices instead of quaternions, to see how W(t) would be defined in terms of matrices.
Mark kindly responded with the following method:
--
Subject: FW: quaternion differentiation
Date: Mon, 24 Jul 2006 18:38:52 +0400
From: "Mark Ioffe"
To: "Martin Baker"
Martin!
Below follows how W(t) would be defined in terms of matrices.
Let
X(t)=X(t0)TX/x(t)
(1)
Where X(t)=any vector of rigid body at moment t
X(t0)=the same vector at moment t0
TX/x(t)= orthogonal matrices
By differentiating (1)
d(Xt)/d(t)= X(t0)d(TX/x(t))/d(t)=
X(t)TX/x(t) (2)
But
d(Xt)/d(t)=[W(t)Xt]
(3)
Where []=cross product of 2 vectors W(t)(angular velocity) and Xt
Cross product of 2 vectors W(t)=(Wx(t), Wy(t), Wz(t)) and Xt can be represented by using antysymmetric matrix
WM(t)=
(4)
[W(t)Xt]=XtWM(t)
(5)
Because Xt is any
vector it follows from (2) and (5)
WM(t)= TX/x(t)
(6)
|
To: "Mark Ioffe"
From: "Martin Baker"
Subject: FW: quaternion differentiation
Date: Tue, 25 Jul 2006 02:08:15 -0700
Mark,
Thank you very much for this, I have put it here:
https://www.euclideanspace.com/physics/kinematics/angularvelocity/index.htm#matrix
There are a few things I'm not clear about, I think its
partly that we are using different notation conventions, and
also the formatting in html.
On the rest of the site I have used the following conventions:
* Right handed cartesian coordinate system
* Right handed screw rule for positive angles
* Right handed vector cross product
* Vectors represented by column
* Matrix multiplication, element is dot product of row in
left hand operand 'dot' column in right hand operand.
* Matrix shown in square brackets
So I would expect something like:
X(t) = [T(t)] X(0)
I cant quite work out this notation:
X(t)=X(t0)TX/x(t)
If you are using a different conventions, I can easily tweek
them to fit in with the rest of the site, but I cant quite
see where the suffix 'X/x' comes from?
Martin
--
Subject: RE: quaternion differentiation
Date: Tue, 25 Jul 2006 18:00:37 +0400
From: "Mark Ioffe"
To: "Martin Baker"
Martin!
Our differences are:
* Vectors represented by row=20
* Matrix shown in round brackets if I show its elements and without =
brackets else
The suffix 'X/x' is subscript for matrix T. It means transition from =
unmoving right handed Cartesian coordinate system OXYX to
moving right handed Cartesian coordinate system Oxyz
Mark.