As discussed on the Noether Theorem page, the conservation of momentum is derived from the symmetry of space, this page defines momentum and explains how it is conserved.
| Conservation Law | Symmetry |
| linear momentum | The laws of physics are the same regardless of our position when we do an experiment. |
| angular momentum | The laws of physics are the same regardless of the direction that we are facing. |
linear momentum
Linear momentum is here denoted by the symbol p, for a solid body:
p = mv
| where: | |||
symbol |
description |
type |
units |
| p | linear momentum | vector | kg m/s |
| m | mass | scalar | kg |
| v | linear velocity | vector | m/s |
p and v are vectors, that is, they have direction and magnitude. Since they are related by a scalar then the direction of p and v is the same.
In the general case, in the 3D world, p and v are 3 dimensional vectors. If we are constrained to a plane then we can use 2D vectors, if we a constrained to a line (i.e. direction is already defined) then we can use scalars.
If a solid body has both linear and angular movement then all the points on the body have a different velocity, in this case the linear velocity is taken to be the linear velocity
Conservation of linear momentum
So far we are talking about a single solid body or particle. We can define the total linear momentum of a set of solid bodies as the sum of all the individual momentums. We just take the vector addition (add each element separately) of all the momentums to give the total momentum for the system. For any closed system this total momentum is constant. Individual bodies within the system may exchange momentum but the total always remains the same. The following pages explain how momentum can be exchanged between bodies by means of forces.
angular momentum
Angular momentum is here denoted by the symbol L, for a solid body:
L = [I]w
| where: | |||
symbol |
description |
type |
units |
| L | angular momentum | bivector | kg m2/s |
| [I] | inertia tensor (moment of inertia) | tensor | kg m2 |
| w | angular velocity | bivector | s-1 |
So [I] is the analog of mass for rotation, this is a tensor, which means that its form depends on the number of dimensions:
- In 1 dimension we cant have rotation, so its not applicable.
- In 2 dimensions rotation only has 1 degree of freedom so [I] is a scalar.
- In 3 dimensions rotation has 3 degrees of freedom and [I] is a 3x3 matrix.
Therefore, in the 3 dimensional case, this adds a lot more complexity than the linear case, for instance:
- The direction (axis of rotation) of w may possibly be different than the direction of the momentum (if [I] has non-zero terms that are not on the leading diagonal) .
- [I] is defined in terms of own local coordinates, this means that its values will change with orientation when we are working in absolute or inertial frame coordinates.
- The total angular momentum of a system depends on which point we measure relative to.
These factors mean that we have to be very careful and rigorous when doing calculations involving angular momentum.
Conservation of angular momentum
In a similar way to linear momentum, we can define the total angular momentum of a set of solid bodies as the sum of all the individual angular momentums. We just take the vector addition (add each element separately) of all the momentums (L is a vector) to give the total momentum for the system, but to do this we must measure the angular momentum relative to the same point and be consistent. For any closed system this total angular momentum is constant. This is conserved completely independently of linear momentum, it is a separate concept. it is therefore not meaningful to talk about converting linear momentum to angular momentum and visa-versa. It is possible for linear motion to be converted to rotational motion and visa-versa, but in any closed system, the total linear momentum and the total angular momentum are both conserved independently.
Total angular momentum of a system of particles.
If a particle can't rotate then can a system of particles have angular momentum?
Centre of mass and first moment of mass
The centre of mass is the point in a solid body which the body would naturally rotate around without external forces.
Centre of mass
This is the point at which we can consider the total mass of the object acts for the purposes of gravity and inertia.
This allows us to ignore the internal structure and forces of the object and to concentrate this all to one point. This assumes the object is solid and that the internal forces within the object are not large enough to distort it.
So the centre-of-mass is like the average position of the mass.
The centre-of-mass of a number of particles relative to an arbitrary point is:
sum(pi * mi)/mt
| where: | |||
symbol |
description |
type |
units |
| pi | relative position of particle i | vector | m |
| mi | mass of particle i | scalar | kg |
| mt | total mass | scalar | kg |
For a continuous object this becomes the first moment of mass:
xcm = ![]() m dx /masstotal
m dx /masstotal
Angular momentum in 2D and second moment of mass
In 2D [I] is a scalar, so we will just use I.
I = sum(pi * mi2)/mt
| where: | |||
symbol |
description |
type |
units |
| pi | relative position of particle i | vector | m |
| mi | mass of particle i | scalar | kg |
| mt | total mass | scalar | kg |
For a continuous object this becomes the first moment of mass:
I = ![]() m2 dx /masstotal
m2 dx /masstotal
Angular momentum in 3D
In 3D [I] is a 3x3 matrix
Angular Momentum of particles( )
)
The instantaneous angular momentum of a particle is the product of its mass and its angular velocity.
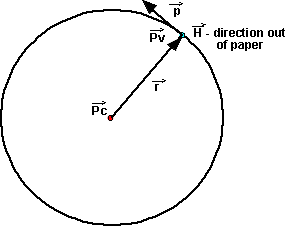
![]() =
= ![]() x
x ![]() =
= ![]() x m
x m![]() =m
=m![]()
| where: | |||
symbol |
description |
type |
units |
| the instantaneous angular momentum about PC | bivector | kg m2/s | |
| x | the cross product operator (see here for definition) | ||
| the instantaneous position of
the particle relative to point. |
vector | m | |
| the instantaneous linear momentum
of the particle = m |
vector | kg m/s | |
| m | the mass of the particle. | scalar | kg |
As with rotation velocity, the angular momentum of a point is not an absolute value, but it depends on which point that the rotation is measured about.
As discussed here, angular momentum of any closed system is conserved. However the particle under consideration here, may have external forces acting on it, so it is not a closed system. When we go on to consider a rigid body rotating about its centre of mass, then the angular momentum of the whole system (about any point) is conserved, this is the sum of the angular momentums of the particles that make up the body. So as it rotates, the instantaneous angular momentum of each particle that makes up the body, will be continuously varying, but the total angular momentum is constant.

