The following pages concern energy and momentum conservation laws. We will define these later, but why are certain quantities like these conserved? Science only allows us to experiment and find how things work, not why, but sometimes science and maths can explain things in terms of a higher level of abstraction, a more general law.
Nothers Theorem says that, for every symmetry exhibited by a physical law, there is a corresponding observable quantity that is conserved.
We can therefore explain the conservation laws in terms of the symmetry of space and time.
| conservation law | symmetry |
|---|---|
| linear momentum | The laws of physics are the same regardless of our position when we do an experiment. |
| energy | The laws of physics are the same regardless of the time that we do an experiment. |
| angular momentum | The laws of physics are the same regardless of the direction that we are facing. |
| The laws of physics are the same regardless of the linear velocity we are traveling when we do the experiment | |
| electric charge | gauge invariance |
Spatial Invariance
This allows us to derive momentum conservation. As we saw on this page we can express the laws of motion in integral form:
momentum = ∫ F dt
This is a line integral in the time dimension which shows us that it is independent of the path through the space dimensions. Therefore the space dimensions are symmetrical.
Time Invariance
This gives us energy conservation. For instance, if gravity changes with time we could raise a weight when gravity is low and release it when gravity is high, the energy output would be higher than energy input, so energy would not be conserved. As we saw on this page we can express the laws of motion in integral form:
energy(work) = ∫ F•dx
This is a line integral in the space dimensions which shows us that it is independent of time. Therefore the time dimension is symmetrical.
Noether for Special Relativity
If we apply this to space-time we get:
symmetry |
conservation law |
The invariant interval
|
Energy-Momentum m2c4=E2 - p2c2 |
| where: | |||
symbol |
description |
type |
units |
 |
invariant interval | scalar | s |
| T | time | scalar | s |
| L | length | vector | m |
| c | speed of light | scalar | m/s |
| m | rest mass | scalar | kg |
| E | energy | scalar | |
| p | momentum | vector | kg m/s |
When the mass is stationary p=0 and the equation becomes;
Energy of stationary mass = m c2
If v is low compared to c the equation becomes:
E = m c2 + p2 /2m + ...
Which is roughly:
E = m c2 + 1/2 m v2
Energy = rest mass + kinetic energy
Noether for Quantum Mechanics
Quantum mechanics tends to deal with the small scale so we will look at the symmetry of fundamental particles:
For Particles (fermions) Angular Momentum is quantized. Particle spin and orbital states are always a half integer multiple of h-bar. In other words,
spin = &
/2, 3*/2 ...
where:
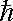- = h/2 PI
- h = Planck's constant
There is also something strange about the spin in that a rotation of 720 (not 360 degrees) is needed to get back to the original orientation. This can be modeled by quaternion (spinor) where a rotation of 360 degrees inverts all of its x,y,z and w elements.
If we take the Schrödinger's wave function for two particles:
ψ (
1,2,t)
We can investigate symmetry by exchanging the two particles:
for two bosons: ψ (1,2,t) = ψ (2,1,t)
for two fermions: ψ (1,2,t) =- ψ (2,1,t)
In other words, if we exchange two identical fermions we invert the wave function. This is equivalent to rotating the system by 180 degrees.
Non Continuous values
Nother even applies to non-continuous values such as reflection.
In this case the measurable physical quantity called parity is conserved.
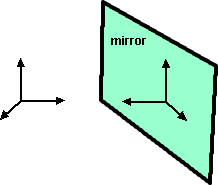
Here are some parity symmetries:
| type | description | |
|---|---|---|
| P | mirror | reflect space in a mirror |
| T | time | replace forward in time with backward in time |
| C | charge | replace particles with a positive charge by a particle with the same properties but with a negative charge and replace negative charge with a positive charge. |
In most cases physics interactions are equally valid when these parity symmetries are applied. However, in some cases they are not, for instance, the weak nuclear force does not obey mirror parity.
There are some particle interactions that are not reversible in time.
However, if we simultaneously reflect in P,T and C then this appears to obey the same laws of physics in that, so far, no exceptions have been found.
